本記事では、PMSMの発生トルクの計算手法について示した後、
所望のdq軸電流を与えてPMSMを駆動するためのシミュレーションモデルや結果の紹介、
シミュレーション結果と出力トルク式の比較について解説しています。
PMSMの出力トルク式
出力トルク式①
出力トルクを計算するためのPMSMの電圧方程式についてはこちらの記事をご覧ください。
PMSMの出力トルクはdq軸電流やモータパラメータを使って以下の式で表されます。
\[T = Pn\{ψ_f+(Ld-Lq)Id\}Iq・・・①\\
Id:d軸電流、Iq:q軸電流、Ra:巻線抵抗、\\
Ld:d軸インダクタンス、Lq:q軸インダクタンス、ψ_f:磁石磁束、\\
Pn:極対数、ω:電気角速度、p:微分演算子\]
出力トルク式②
また、dq軸電流Id、Iqを電流ベクトルIampと電流位相βを用いて(下図)表すと、
以下のように変形できます。
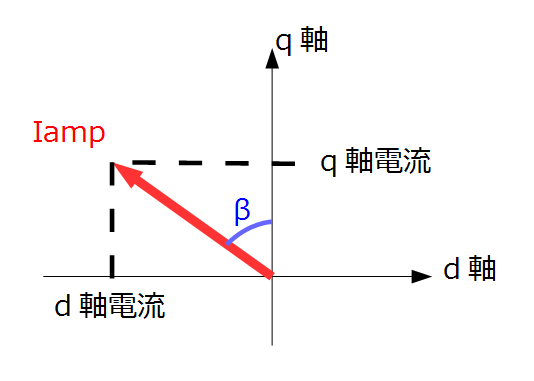
\[ T = Pn\{ψ_f Iamp \cos β-\frac{1}{2}(Ld-Lq)Iamp \sin 2β\}・・・②\]
出力トルク式①の検証
シミュレーションモデル
まずは①のトルク式が正しいか、シミュレーションにより確認してみましょう。
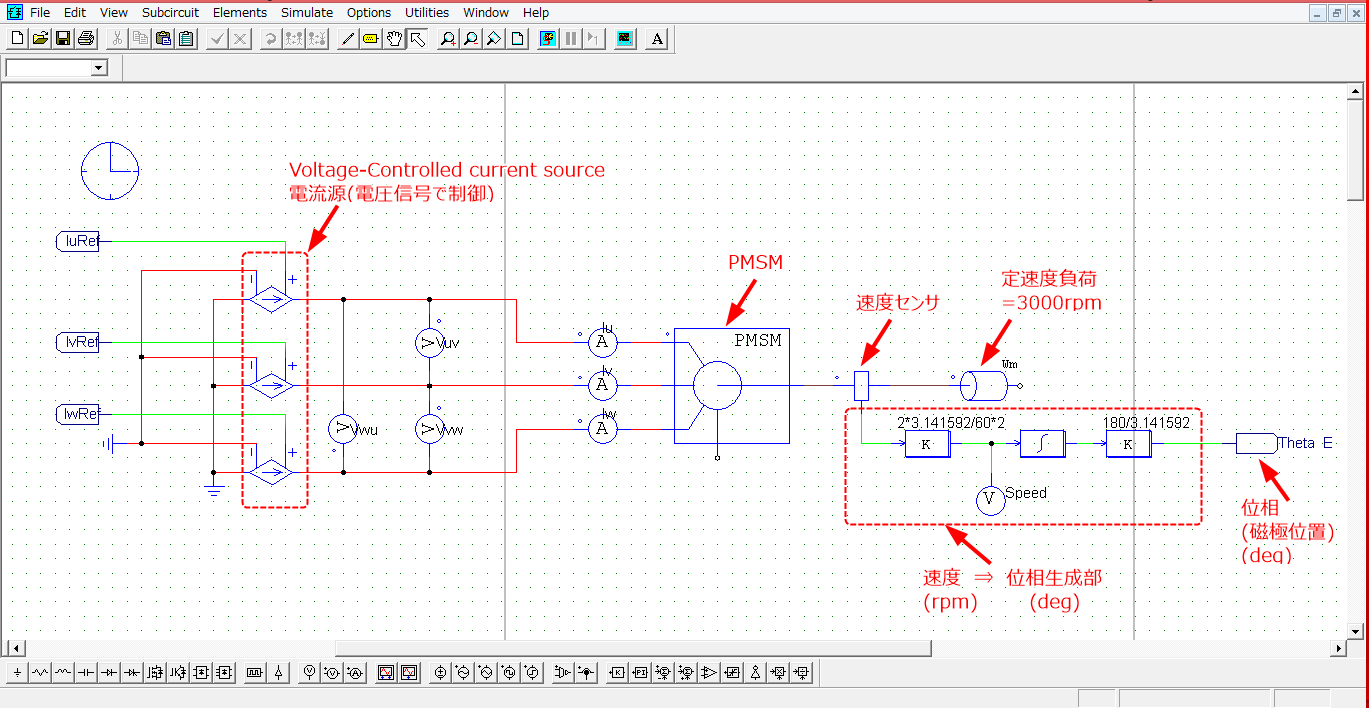
下図のようにPMSMモデルを使用してシミュレーションを行いますが、PSIMのPMSMモデルは
dq軸電流を直接入力することができない(三相入力に対応している)ため、電流源ブロックを用いて
所望のdq軸電流を流すこととしています。
ここでは電流源ブロックとして、Voltage-Controlled current sourceブロックを使用しています。
このブロックは電圧信号を入力すると、入力と相似な電流を流してくれる電流源になります。
以下の式で与えられるdq⇒3相の座標変換を用いて、指定したdq軸電流指令値から三相電流指令値を
生成します。これをVoltage-Controlled current sourceブロックに入力することで、PMSMには
指定したdq軸電流を流し続けることができます。
\[
\begin{pmatrix}
Iu \\
Iv \\
Iw
\end{pmatrix}=
\begin{pmatrix}
cosθ&sinθ \\
cos(θ-\frac{2}{3}π)&sin(θ-\frac{2}{3}π) \\
cos(θ+\frac{2}{3}π)&sin(θ+\frac{2}{3}π)
\end{pmatrix}
\begin{pmatrix}
Id \\
Iq
\end{pmatrix}
\]・・・③
下図が主回路のモデルで、それぞれのパラメータは以下になります。
※PMSMブロックはLd=Lqで突極性がないモデルを使用している点にご注意ください。
【PMSMブロック】
Rs: 0.5(Ω)
Ld: 0.027(H)
Lq: 0.027(H)
Vpk/krpm:296.1921959 (①、②におけるψf=1.0相当)
No. of Poles P: 4
Moment of Inertia: 0.0179 (kg*m2)
Mech. Time Constant: 10
Torque Flag:1:出力あり
Master/Slave: 1:マスタ
【Mechanical Load(constant-speed):定速度負荷】
Constant Speed(rpm):3000
Moment of Inertia:0
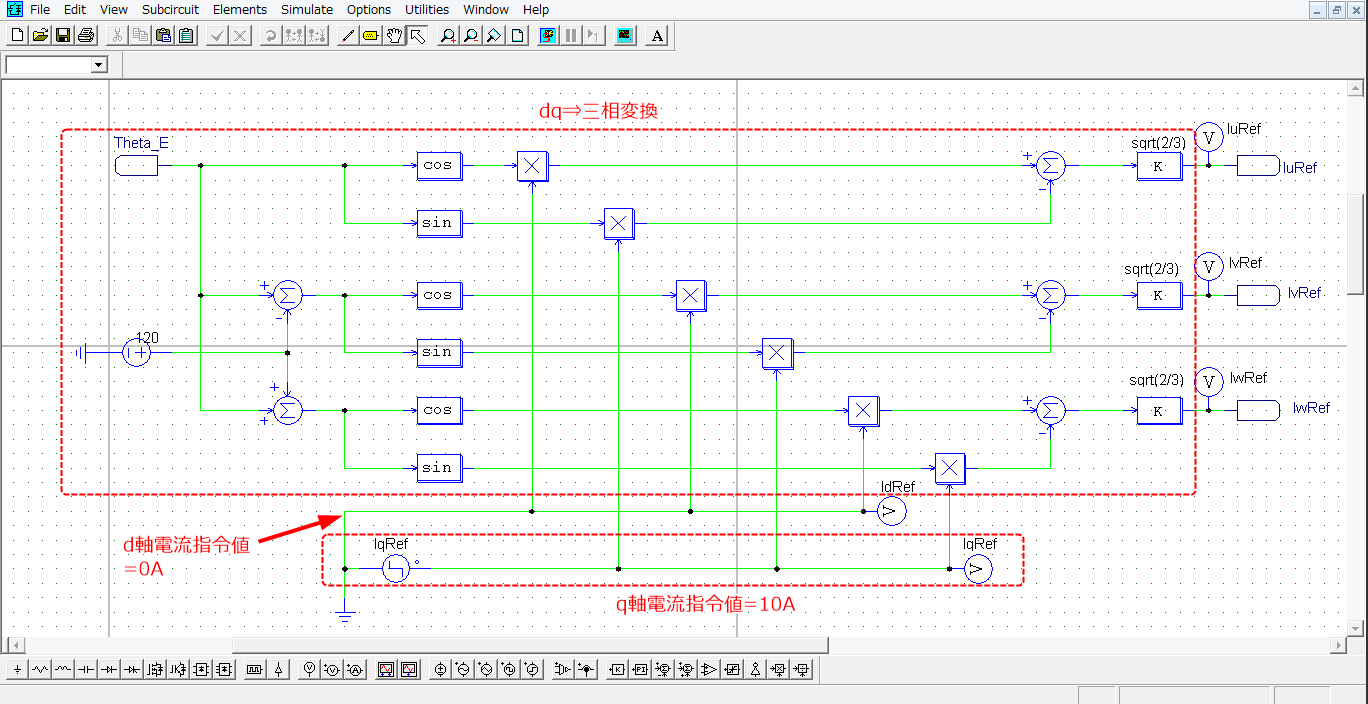
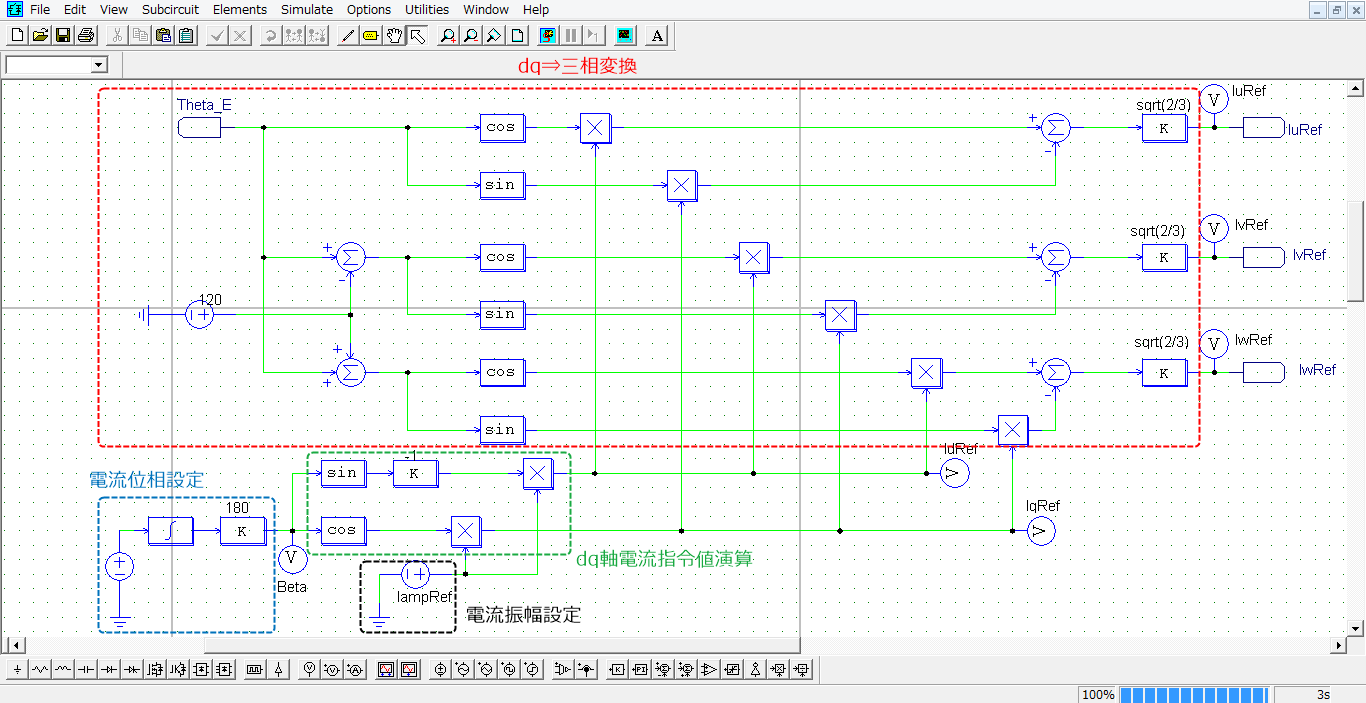
続いて、制御部のモデルを下図に示します。
(※上図の速度センサでの検出値から位相を生成する部分も制御部になります)
【位相生成部】
ここではdq⇒三相変換に使用するためのモータの位相(回転子のN極の位置)を生成します
(③式のθに使う部分を生成することになります)。
速度センサは現在の速度N(rpm)検出します。次元:(rpm)のため、まずは以下の式により電気角速度ωe(rad/s)に変換します。その後、積分することでモータ位相θe(rad)を生成します。
※なお、PSIMの三角関数ブロックへの位相入力は次元:(deg)で入力する必要があり、
ここで180/πを掛けて、次元を変換しています。
\[ω_e = \frac{2π}{60}PnN・・・④\]
【dq⇒三相変換】
dq軸電流指令値と【位相生成部】で生成した位相を入力して三相の電流指令値を生成します。
【dq軸電流指令値】
\[d軸電流指令値=0A\\
q軸電流指令値=\{
\begin{matrix}
0A (0≦t<0.2)\\
10A (0.2≦t)
\end{matrix}\]
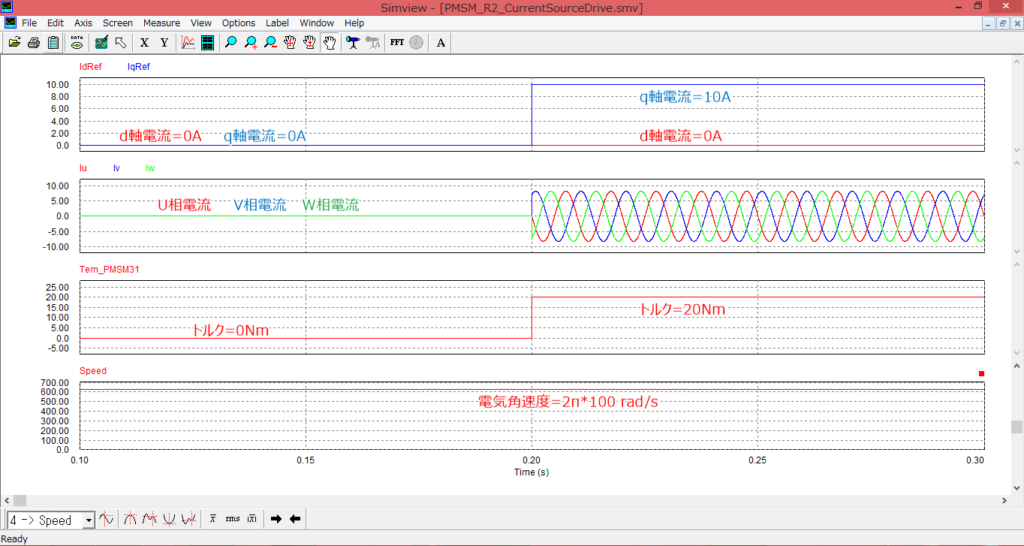
シミュレーション結果
シミュレーション結果を以下に示します。
上からdq軸電流 / UVW相電流(三相電流) / トルク / 電気角速度
を表しています。
q軸電流が0.2sから10Aに立ち上がり、dq⇒三相変換により三相電流指令値が生成され、
電流源(Voltage-Controlled current source)によりPMSMへ電流を流し込まれることで、
トルクが発生しています。
トルクの大きさについて、①から確認してみましょう。今回の条件ではPMSMのLd=Lqとしている、
かつ、d軸電流指令値を0Aとしているため、①の第二項は0となります。
そのため、第一項を計算すると、以下のようになります。
\[T = Pn\{ψ_f+(Ld-Lq)Id\}Iq = 2 * 1.0 * 10 = 20 (Nm)\]
このようにシミュレーション結果の発生トルクとも一致することを確認できました。
出力トルク式②の検証
シミュレーションモデル
主回路のモデルは「出力トルク式①」と同様になるので省略します。
制御部のモデルは一部変更して、下図のようになります。
【位相生成部】と【dq⇒三相変換】は「出力トルク式①の制御部モデル」と同じになります。
【電流振幅設定】
電流振幅Iamp=100A
【電流位相設定】
電流位相β=0deg ⇒ 360degまで、0.5sかけてスロープ状に増加するように設定
【dq軸電流指令値演算】
以下の式でd軸電流指令値IdRef、q軸電流指令値IqRefを生成しています。
\[ \begin{matrix}
IdRef = – Iamp sinβ\\
IqRef = Iamp cosβ
\end{matrix}・・・④\]
シミュレーション結果
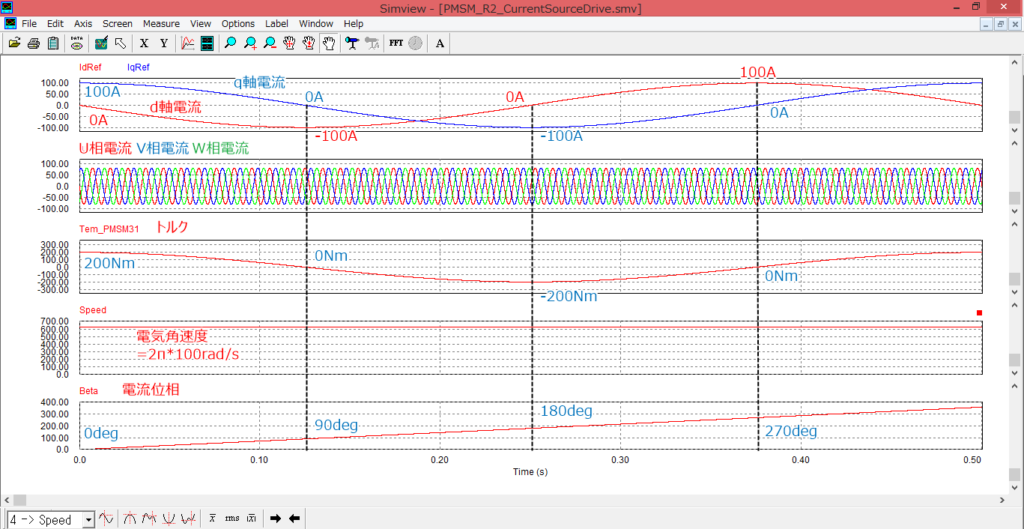
シミュレーション結果を以下に示します。
上からdq軸電流 / UVW相電流(三相電流) / トルク / 電気角速度 / 電流位相
を表しています。
電流位相が0deg⇒360degに回転するにしたがって、d軸電流は-SIN関数、q軸電流はCOS関数
で変化していることがわかります。
dq軸電流の変化は④式から説明できます。
出力トルクもq軸電流と相似な変化をしており、トルクの変動幅も±200Nmとなっており、q軸電流の変動幅が±100Aであること、さらに②式と併せて、以下のように計算できます。
※出力トルク式①の場合と同様にLd=Lqであるため、第二項は0になります。
\[T = Pn\{ψ_f Iamp \cos β-\frac{1}{2}(Ld-Lq)Iamp \sin 2β\} = 2*1.0*100*cosβ\]
以上のように所望のdq軸電流をPMSMに流し込むことによりトルクを発生させることができ、
出力トルク式①や②により発生しているトルクを計算できることをシミュレーションにより
確認しました。
お疲れさまでした!

コメント