制御工学の基礎~ベクトル軌跡は何を示しているのか~

本記事では制御工学において周波数応答の解析を行うために使用されるベクトル軌跡の概要、描画の方法、具体的な制御要素を対象としたベクトル軌跡を示すことにより、ベクトル軌跡が何を示すのかを解説しています。

ベクトル軌跡とは
代表的なベクトル軌跡
まとめ

ベクトル軌跡とは

周波数伝達関数\(G(jω)\)は複素数であるから、角周波数\(ω\)に対して、
\[G(jω)=Re(ω)+j・Im(ω)\]
のように実数部と虚数部によって複素平面上に表示できます。
つまり、以下の絶対値\(|G(jω)|\)、偏角\(\angle G(jω)\)
\[|G(jω)|=\sqrt{Re^2(ω)+Im^2(ω)}\\
\phi = \tan^{-1}\frac{Im(ω)}{Re(ω)}\]
のベクトルの先端を示しています。
図にすると下図になります。
※周波数伝達関数についてはこちらの記事もご参照ください

用語解説

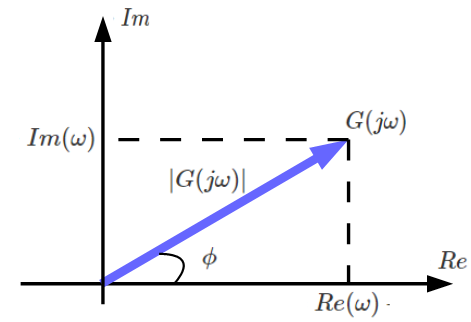
この時、絶対値\(|G(jω)|\)、偏角\(\angle G(jω)\)は以下を示しています。
\(G(jω)\)の形で表現される制御要素に入力される信号(入力信号)と制御要素から出力される信号(出力信号)について
□絶対値\(|G(jω)|\)：出力信号と入力信号の振幅比(ゲインともよびます)
□偏角\(\angle G(jω)\)：入力信号と出力信号の位相差

ここで、\(ω\)を\(ω=0\)から\(ω=\infty\)まで変化させるとベクトルの先端は複素平面上に直線または曲線を描きます。これをベクトル軌跡と呼びます。ベクトル軌跡には\(ω\)の増大方向に矢印を付けて必要に応じて\(ω\)の値を記入して表現します。

POINT

周波数伝達関数を複素平面上に表示するとベクトルの先端を表す。
このベクトルを\(ω=0\)から\(ω=\infty\)へ変化させて描いた直線または曲線がベクトル軌跡。

代表的なベクトル軌跡

本章では代表的な周波数伝達関数のベクトル軌跡を紹介していきます。

微分要素/積分要素

【微分要素】
□伝達関数\[G(s)=sK\]
□周波数伝達関数\[G(ω)=j・ωK\]
□ゲイン/位相差
\[|G(jω)|=ωK\\
\phi = 90°\\
※実数部=0かつ虚数部>０のため、90° 一定\]

【積分要素】
□伝達関数\[G(s)=\frac{K}{s}\]
□周波数伝達関数\[G(ω)=\frac{K}{j・ω}=-j・\frac{K}{ω}\]
□ゲイン/位相差
\[|G(jω)|=\frac{K}{ω}\\
\phi = -90°\\
※実数部=0かつ虚数部<０のため、-90° 一定\]

POINT

【微分要素】
□入力信号の周波数によらず90°位相が進んだ信号を出力
□入力信号の周波数が高いほど、ゲインが大きい(出力信号の振幅が大きい)
【積分要素】
□入力信号の周波数によらず90°位相が遅れた信号を出力
□入力信号の周波数が高いほど、ゲインが小さい(出力信号の振幅が小さい)

一次遅れ要素

一次遅れ要素の周波数伝達関数を以下に示します。
\[G(jω)= \frac{K}{1+j・ωT}=\frac{K}{1+ω^2T^2}-j・\frac{K・ωT}{1+ω^2T^2}\]
よってゲインと位相差は以下のようになります。
\[|G(jω)|=\frac{K}{\sqrt{1+ω^2T^2}}\\
\phi = \tan^{-1}(-ωT)\]
\(K=1、T＝１\)として\(ω=0\)から\(ω=\infty\)まで変化させたベクトル軌跡は下図(左)のようになります。また、ベクトルを投影すると下図(右)のようになります。

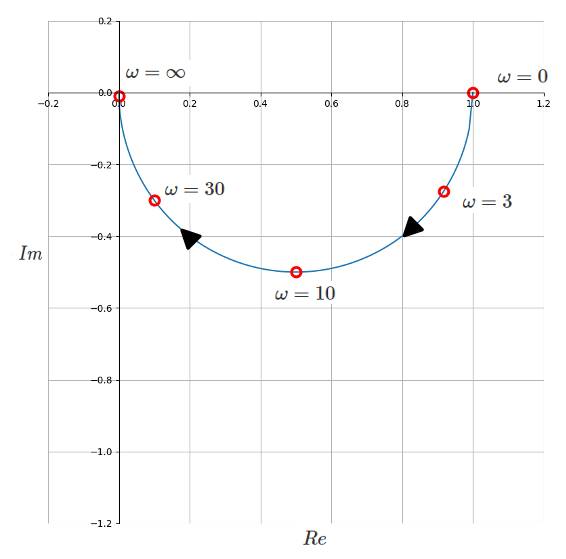
\(ω=0\)では\((Re,Im)=(1,0)\)からスタートして、\(ω\)の増大に伴い半円を描きながら\(ω=\infty\)で原点に到達していることがわかります。

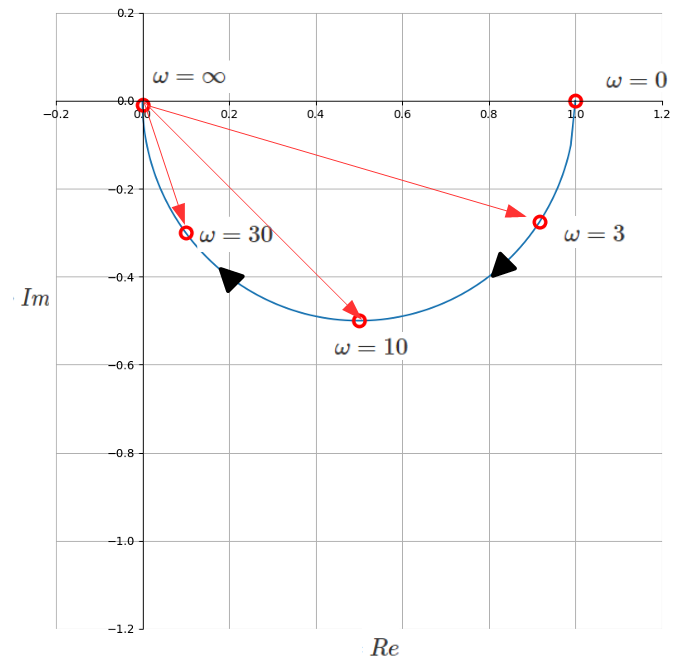
ベクトルを投影すると\(ω\)の増大によってゲインが小さく、位相差は大きくなっていることがわかります。

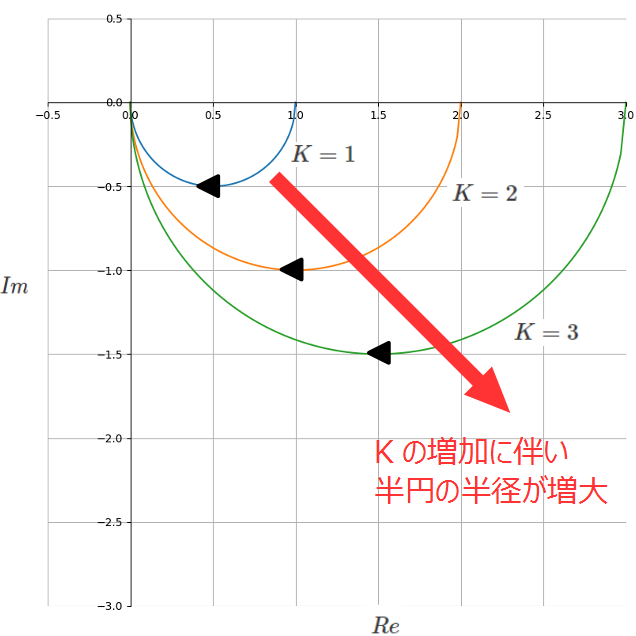
次に\(K\)の値を変えていった場合のベクトル軌跡を示します。
\(K\)の値が大きくなるほど、半円の面積が大きくなっていることがわかります。

POINT

□ベクトル軌跡は半円、周波数の増加によりゲインが小さく、かつ位相遅れが大きくなる
　(周波数が高いほど入力信号に対して出力信号の振幅が小さく、位相差が拡大)
□周波数伝達関数の分子Kが大きいほど半円の半径が大きくなる

二次遅れ要素

二次遅れ要素の周波数伝達関数を以下に示します。
(※二次遅れ要素についてはこちらの記事もご参照ください)
\[G(jω)=\frac{ω_n^2}{(jω)^2+2ζω_n(jω)+ω_n^2}\]
分母分子を\(ω_n^2\)で割ると、
\[G(jω)=\frac{1}{(1-\frac{ω^2}{ω_n^2})+j・2ζ\frac{ω}{ω_n}}\]
\[=\frac{1-\frac{ω^2}{ω_n^2}}{(1-\frac{ω^2}{ω_n^2})^2+4ζ^2 \frac{ω^2}{ω_n^2}}-j・\frac{2ζ \frac{ω}{ω_n}}{(1-\frac{ω^2}{ω_n^2})^2+4ζ^2\frac{ω^2}{ω_n^2}}\]
よってゲインと位相差は以下のようになります。
\[|G(jω)|=\frac{1}{\sqrt{(1-\frac{ω^2}{ω_n^2})^2+4ζ^2\frac{ω^2}{ω_n^2}}}\\
\phi = -\tan^{-1}\frac{-2ζ \frac{ω}{ω_n}}{1-\frac{ω^2}{ω_n^2}}\]
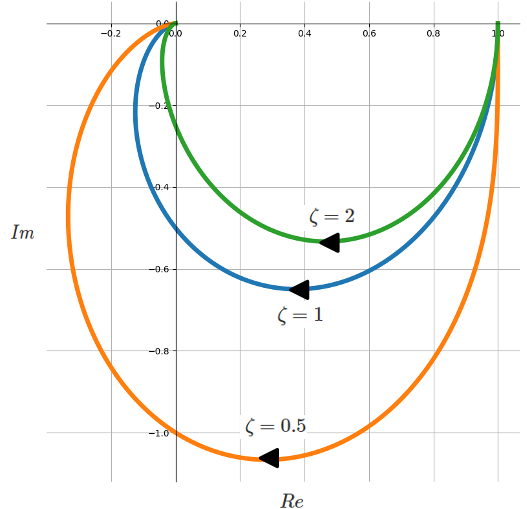
まずは\(ω_n = 600rad/s\)に固定した状態で、減衰定数を\(ζ=0.5、1、2\)と変えていった場合のベクトル軌跡を示します。
\(ζ\)によらず曲線を描いていますが、\(ζ\)が大きくなるにしたがって、ゲインが小さくなっていることが読み取れます。

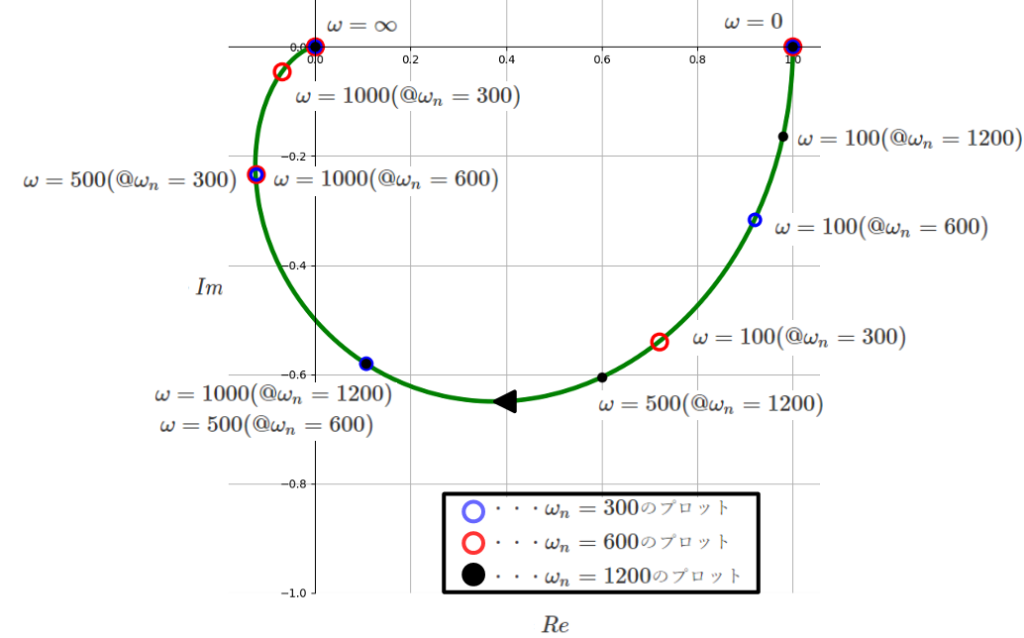
次に\(ζ=1\)に固定した状態で固有角周波数\(ω_n = 300、600、1200rad/s\)と変えていった場合のベクトル軌跡を示します。
ベクトル軌跡は\(ω_n\)が変わっても同様であるため、\(ω_n\)毎のプロットを示しています。
入力信号の周波数が高いほど、位相遅れが拡大していく特性は同じですが、\(ω_n\)が大きいほど、周波数の増大に対して、位相遅れが拡大しづらいことが読み取れます。