本記事では過渡現象について説明した後、過渡現象の解析方法として、数式を立式して
回路上の電圧、電流を計算する方法、PSIMを使ったシミュレーションで解析を行う方法
について解説しています。
過渡現象とは
電気回路がある一定条件の下、十分長時間置かれている場合、回路内の電流/電圧は時間的に
一定で、変わらない状態となっている(これを定常状態という)。
これに対して、回路に印加する電圧を変えたり、回路内の抵抗値が変化する場合には
ある定常状態から、別の定常状態へ移行する。
また、回路にインダクタンスやキャパシタのような誘導性、容量性の素子が含まれる場合、
一般的には変化に時間を要することが知られている。
この変化の過程を過渡現象という。
回路解析
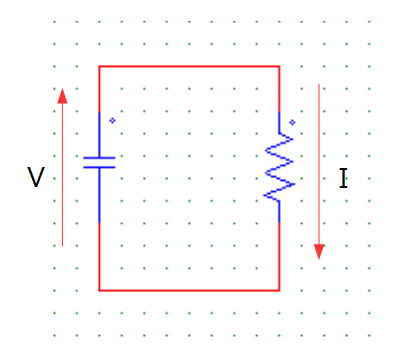
今回は下図のRC回路を使用して過渡現象の解析方法について説明します。
下図のように電流Iと電圧Vをおいて、回路の方程式を求めると以下のようになります。
なお、抵抗値をR、キャパシタ容量をCとおいて式を記述しています。
\[I = C\frac{dV}{dt} ・・・①\]
\[V = RI・・・②\]
①と②から以下の微分方程式を導出でき、回路を流れる電流はこの微分方程式を
解くことで求められます。
\[RC\frac{dI}{dt}-I=0・・・③\]
定常的にはdI/dtの項は0になるので、定常解Is=0
一方の過渡解Itは以下のように求めることができる
\[It = Aexp(-\frac{1}{RC}t)・・・④\]
定常解Is=0なので、I=Itとなる。ここでAは積分定数なので、初期条件から求めることができる。
t=0の時の電圧値をVoとすると、⑤のようになる。
\[It = A=\frac{V}{R}・・・⑤\]
これを④に代入すると電流は⑥、電圧は⑥を②へ代入して求めることができる
\[I = \frac{Vo}{R}exp(-\frac{1}{RC}t)・・・⑥\\V = Vo\exp(-\frac{1}{RC}t)・・・⑦\]
シミュレーションモデル
計算した結果が合っているか確認するため、シミュレーションを行っていきます。
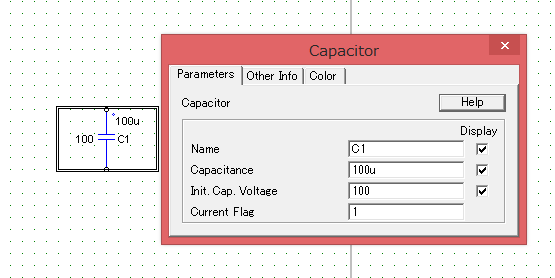
RC回路の内、Cについては下図のように設定しておきます。
※キャパシタの初期電圧(⑥、⑦のVoについては今回は100Vに設定)
【キャパシタ】
Capacitance=100μF
Init.Cap.Voltage = 100V(これが初期電圧の設定パラメータになります)
Current Flag = 1
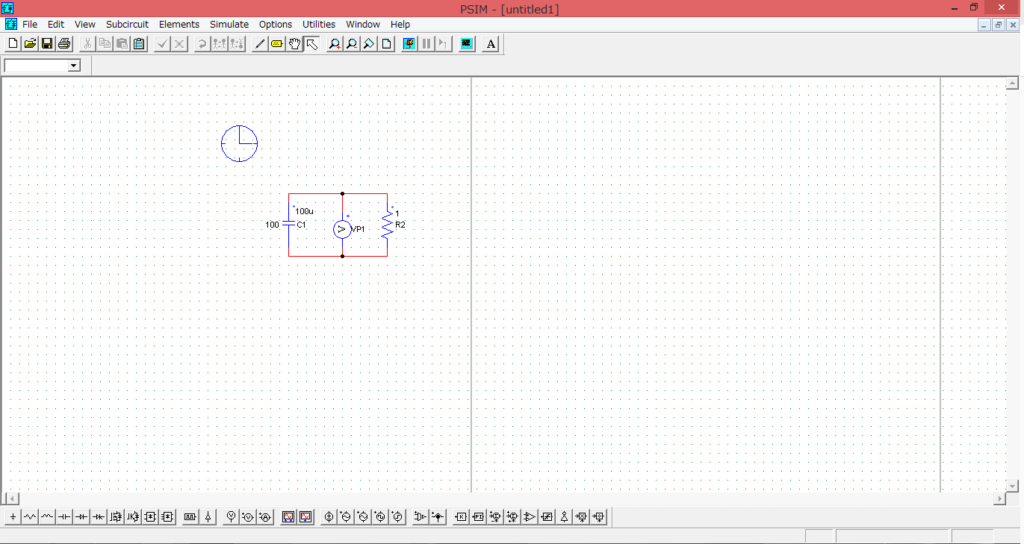
抵抗とキャパシタの両端の電圧を観測するための電圧計、Simulation Control(時計のブロック)を
配置してシミュレーション回路を作成していきます。
抵抗とSimulation Controlの設定は以下の通りです。
【抵抗】
Resistance=1Ω
Current Flag = 0
【Simulation Control】
Time step = 1e-5
Total time = 0.01
Print time = 0
Print step = 1
Load flag = 0
Save flag = 0
シミュレーション結果
シミュレーション回路が完成したので、シミュレーションを実行します。
結果、下図のような波形になりました。
電圧、電流ともに十分時間が経った定常状態では0V,0Aになっていることがわかります。
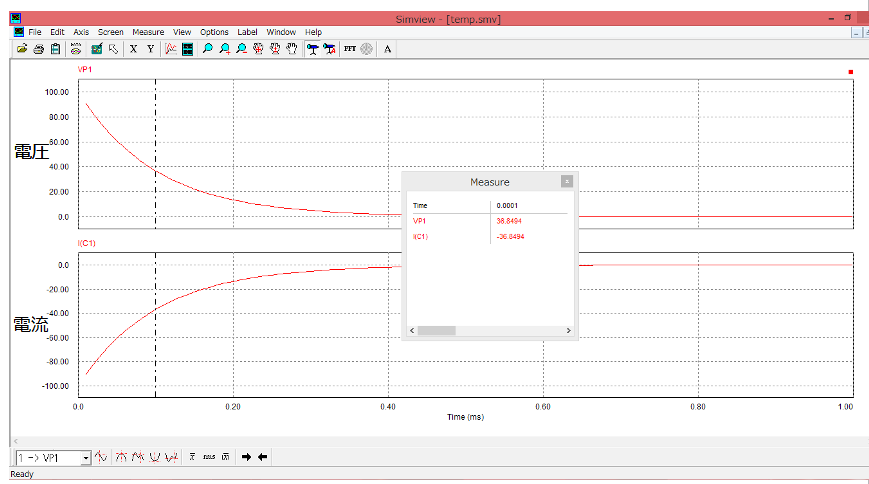
過渡的な応答について確認するため、0~1msの間を拡大して表示してみます。
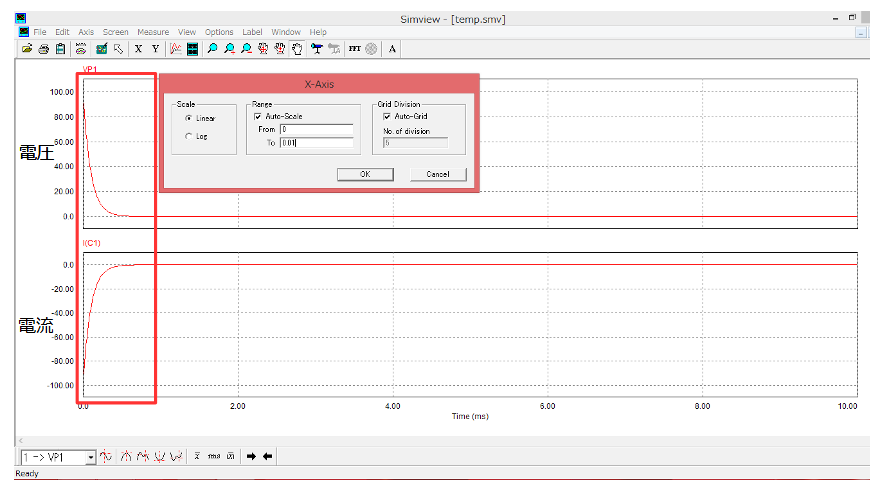
拡大波形を見てみると。。。
【電圧】
初期値Vo=100V(シミュレーション刻みである10μs後から波形が表示されるため、
0sの波形は表示されていません)
点線の位置の値を確認してみると36.8V程度。この値について⑦を使って考えてみましょう。
\[V = Vo\exp(-\frac{1}{RC}t)・・・⑦(再掲)\]
時間t=RCであれば⑦は以下のようになります。
今回の場合だとR=1Ω,C=10μFなので、t = RC = 10μsの時に36.78Vとなり、
シミュレーションと概ね一致していることがわかりました。
なお、ここで計算したRCは回路時定数と呼ばれ、過渡現象の応答速度の指標として知られています。
\[V = Vo\exp(-1)=36.78 V\]
【電流】
電流も同様に考えることができます。
初期値:Vo/R=100A とすると、t=10μsの時点の電流値は36.8A程度となり、
シミュレーション結果からも上記の内容が確認できます。
今回は過渡現象の計算方法とPSIMを使ったシミュレーション方法について解説しました。
お疲れさまでした!


コメント