制御工学の基礎~安定な制御系とは？安定な条件とは？~

本記事では制御系の安定性についての説明と安定であるための条件について例題を交えながら解説を行っています。

安定性の概要
1. 安定/不安定であるとは
2. 安定である条件
フィードバック制御系の安定性
1. フィードバック制御系が安定な条件とは
2. 例題
まとめ

安定性の概要

安定/不安定であるとは

本記事で扱っている制御(自動制御)の目的とは、制御量を目標値に一致させることにあります。
そのため、目標値に変化が発生したり、外乱が入ってきたりしたとしても時間の経過とともに平衡状態に落ち着く必要があります。
ここで、そして、制御系は以下のように安定/不安定の状態に分けることができます。

安定：目標値の変化や外乱の影響を受けたとき、時間の経過とともに再び平衡状態に収束
不安定：目標値の変化や外乱の影響を受けたとき、時間の経過によりますます平衡状態から離れる

この安定/不安定を二次遅れ要素を例にとって説明します。
以下に二次遅れ要素を二通り示します。それぞれにステップ入力を与えた場合の応答(ステップ応答)について確認してみましょう。

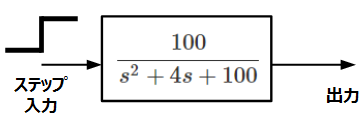
ステップ応答
\[y(t) = \\1-e^{-2t}(\cos{4\sqrt{6}t}+\frac{1}{2\sqrt{6}}\cos{4\sqrt{6}t})\]

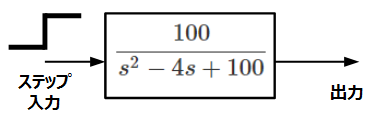
ステップ応答
\[y(t)=\\1-e^{2t}(\cos{4\sqrt{6}t}-\frac{1}{2\sqrt{6}}\cos{4\sqrt{6}t})\]

左側の場合、ステップ入力した場合の式は以下のようになります。
\[\frac{100}{s^2+4s+100}・\frac{1}{s}\\=\frac{1}{s}-\frac{(s+4)}{s^2+4s+100}\\=\frac{1}{s}-\{\frac{(s+2)+2}{(s+2)^2+96}\}\\=\frac{1}{s}-\frac{s+2}{(s+2)^2+96}-\frac{\sqrt{96}・\frac{2}{\sqrt{96}}}{(s+2)^2+96}\]
出力\(y(t)\)を求めるためにラプラス逆変換すると
\[y(t)=1-e^{-2t}(\cos{4\sqrt{6}t}+\frac{1}{2\sqrt{6}}\cos{4\sqrt{6}t})\]
と求められます。
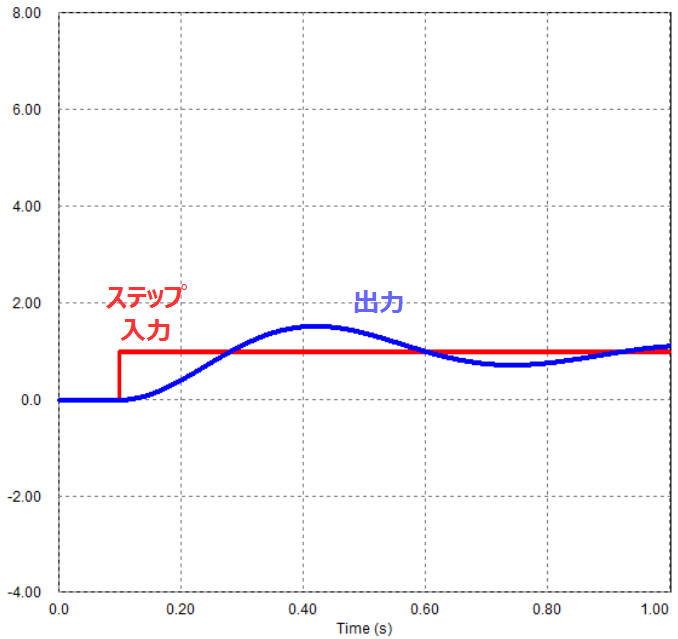
時間経過とともに一致値に収束する安定な系であることが式、時間応答波形からも確認できます。
この応答は以前の二次遅れ要素に関する記事における\(ζ=2\)の場合に相当します。

一方、右側の場合も同様に計算すると、以下のようになります。
\[\frac{100}{s^2-4s+100}・\frac{1}{s}\\=\frac{1}{s}-\frac{s-2}{(s-2)^2+96}+\frac{\sqrt{96}・\frac{2}{\sqrt{96}}}{(s-2)^2+96}\]
こちらも、出力\(y(t)\)を求めるためにラプラス逆変換すると
\[1-e^{2t}(\cos{4\sqrt{6}t}-\frac{1}{2\sqrt{6}}\cos{4\sqrt{6}t})\]
となります。
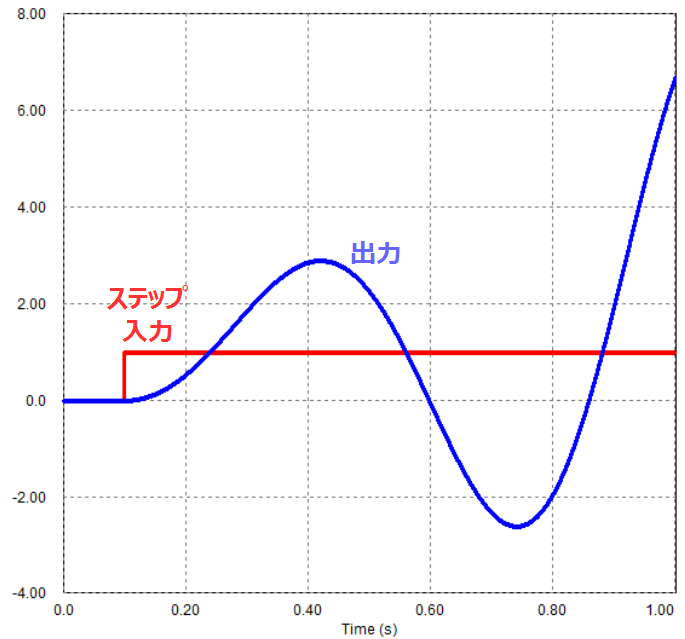
こちらの場合、時間の経過とともに平衡状態に落ち着かず、発散してしまう不安定な系であることがわかります。

安定である条件

前章の例の伝達関数の極に着目すると、
安定な場合：\(s=-2±4\sqrt{6}\)
不安定な場合：\(s=2±4\sqrt{6}\)
となっていることがわかります。
以下のように極\(p_1、p_2\)を持つ伝達関数\(G_1(s)\)を考えてみます。
\[G_1(s)=\frac{1}{s-p_1}・\frac{1}{s-p_2}\]
この\(G_1(s)\)にステップ入力をした場合のステップ応答を考えてみます。
\[\frac{1}{s-p_1}・\frac{1}{s-p_2}・\frac{1}{s}\\=\frac{1}{p_1(p_1-p_2)}・\frac{1}{s-p_1}+\frac{1}{p_2(p_2-p_1)}・\frac{1}{s-p_2}+\frac{1}{p_1p_2}・\frac{1}{s}\]
これをラプラス逆変換すると時間応答\(y_1(t)\)が求まります。
\[y_1(t)=\frac{1}{p_1(p_1-p_2)}・e^{p_1t}-\frac{1}{p_2(p_1-p_2)}・e^{p_2t}+\frac{1}{p_1p_2}\]
\(e\)の右上の指数部分に極\(p_1、p_2\)が現れているのが確認できます。
極の実数部が負であれば、\(e^{p_1t}、e^{p_2t}\)は十分に時間が経つと、つまり\(t⇒∞\)となると0になるため、\(y_1(t)=\frac{1}{p_1p_2}\)となり、一定値に収束します。
一方で、極の実数部が正の場合、\(t⇒∞\)とした時の\(e^{p_1t}、e^{p_2t}\)はそれぞれ\(∞\)に発散してしまい、不安定であることが分かります。
このように安定であるためには、極の実数部が負である、つまり複素平面の左半分にすべての極が存在する必要があります。

POINT

安定=時間の経過とともにある平衡状態に収束
すべての極の実数部が負、つまり複素平面の左半分に存在すれば安定

フィードバック制御系の安定性

フィードバック制御系が安定な条件とは

以下のフィードバック制御系において、

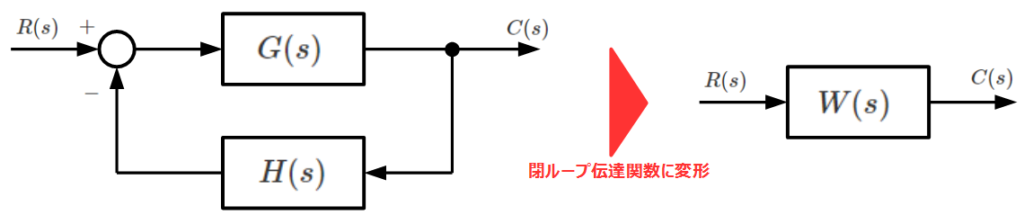
閉ループ伝達関数\(W(s)\)の極を調べれば安定性について確認できます。
\[W(s) = \frac{G(s)}{1+G(s)H(s)}\]
となりますが、\(G(s)、H(s)\)はそれぞれsの多項式の比として、
\[G(s) = \frac{q(s)}{p(s)}\\H(s)= \frac{q_h(s)}{p_h(s)}\]
と表されるため、
\[W(s) = \frac{\frac{q(s)}{p(s)}}{\frac{q(s)*q_h(s)}{p(s)*p_h(s)}}\\=\frac{p(s)*q_h(s)}{p(s)*p_h(s)+q(s)*q_h(s)}\]
となるので、\(W(s)\)の極は特性方程式
\[p(s)*p_h(s)+q(s)*q_h(s)=0\]
の根となり、つまりこれは
\[1+G(s)H(s)=0\]
の根となります。
よって、フィードバック系が安定であるための条件は上記の特性方程式のすべての根の実数部が負となることであります。

例題

下図のようなフィードバック制御系の安定性を求めてみましょう。
(目標値：\(R(s)\)、出力：\(C(s)\)、偏差：\(E(s)\))

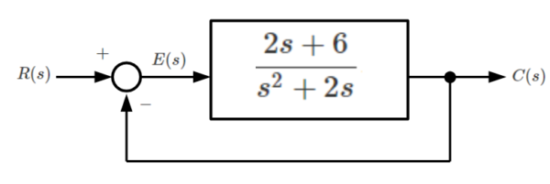
\[G(s)=\frac{2s+6}{s^2+2s}、H(s)=1\]
であるので、特性方程式\(1+G(s)H(s)=0\)は以下のようになります。
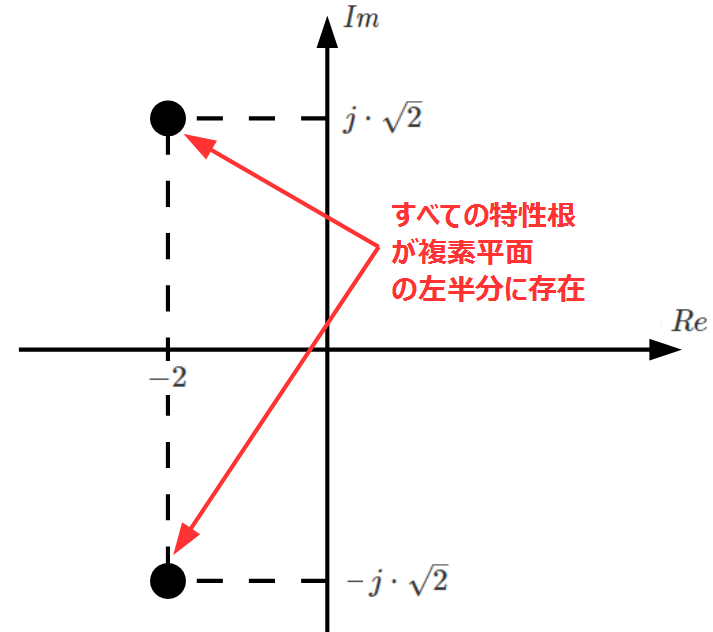
\[1+\frac{2s+6}{s^2+2s}=0\\ \Leftrightarrow \frac{s^2+4s+6}{s^2+2s}=0\\ \Leftrightarrow s = -2±j・\sqrt{2} \]
下図のようにすべて複素平面の左半分に特性根が存在するため、安定となります(下図左)。
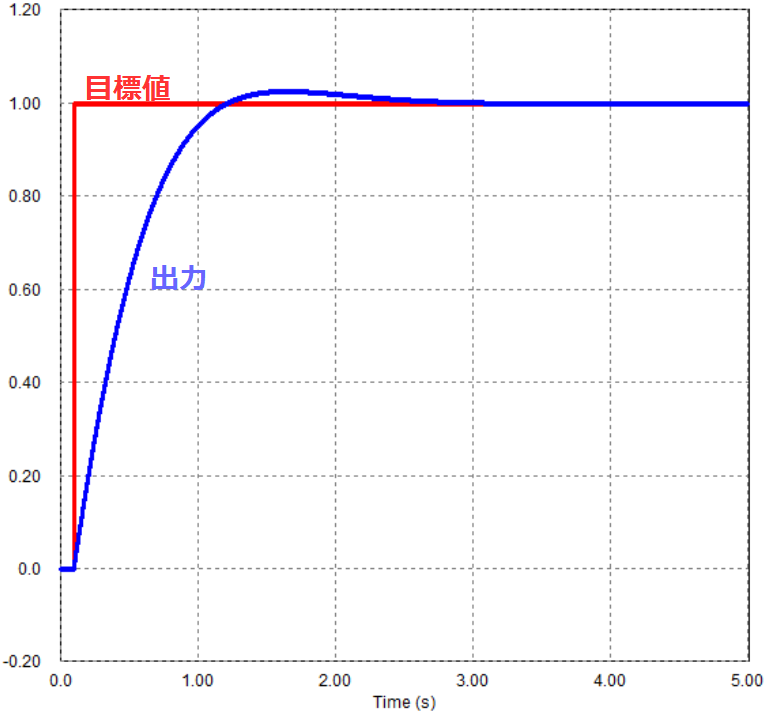
また、確認のため、目標値\(R(s)\)にステップ入力を与えた場合にも出力\(C(s)\)は不安定にならず、目標値に一致していることがわかります。