インバータ工学~三角波比較PWMと三次調波重畳の方法~

本記事では以下の内容について解説を行っております。
□三角波比較型のPWM方式を利用した三相インバータの電圧制御手法
□三相インバータの出力電圧を増加させる(電源の電圧利用率を向上させる)ための三次調波重畳方式
□三次調波方式の有無による動作波形比較

三相インバータとPWM方式

三相インバータ回路の制御法

以下のような三相インバータ回路を考えてみましょう。直流電圧源からの直流電力を三相電力に変換(電力変換)してRL負荷に供給します。電力変換には適切なタイミングで6個のスイッチング素子のオンオフを制御する必要があり、本記事では三角波比較型のPWM方式について解説します。
※制御手法は他にも様々存在します。

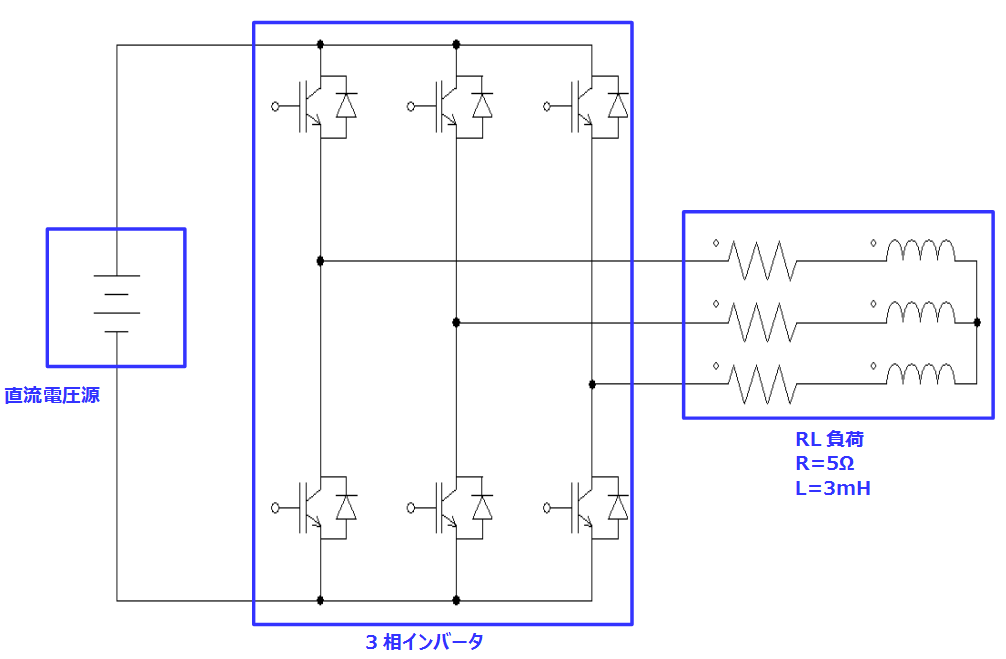
三角波比較型のPWM制御方式では下図のように電圧指令値と三角波キャリアの比較により、スイッチング素子のON/OFFを制御するゲート信号を生成します。
(下図はU相1相分の波形ですが、三相インバータの場合はそれぞれ120°ずれのV相、W相の電圧指令値に対しても、同様に三角波キャリアとの比較でPWM波形を生成します。)
このゲート信号でインバータ各相のスイッチング素子のON/OFFを制御して、等価的に指令値通りの正弦波が得られるように制御を行う手法となっています。
※ここまでの内容はこちらの記事を参考にさせていただいております。

PWMによる三相インバータの制御例

上図のインバータ回路を例に、PWM制御でどのように電圧が制御されるかを確認してみましょう。
【条件】
□電圧指令値：ピーク値0.5Vの正弦波
□三角波キャリア：ピーク値1.0V
□直流電圧：650V

なお、電圧指令値と三角波キャリアのピーク値の比率(電圧指令値/三角波キャリア)は変調率と呼ばれ、直流電圧(電源電圧)の利用率を示す指標の一つとして用いられます。
(※ただし、変調率の定義は書籍、サイトによって異なるのでご注意ください)
今回の条件の場合、変調率0.5となります。

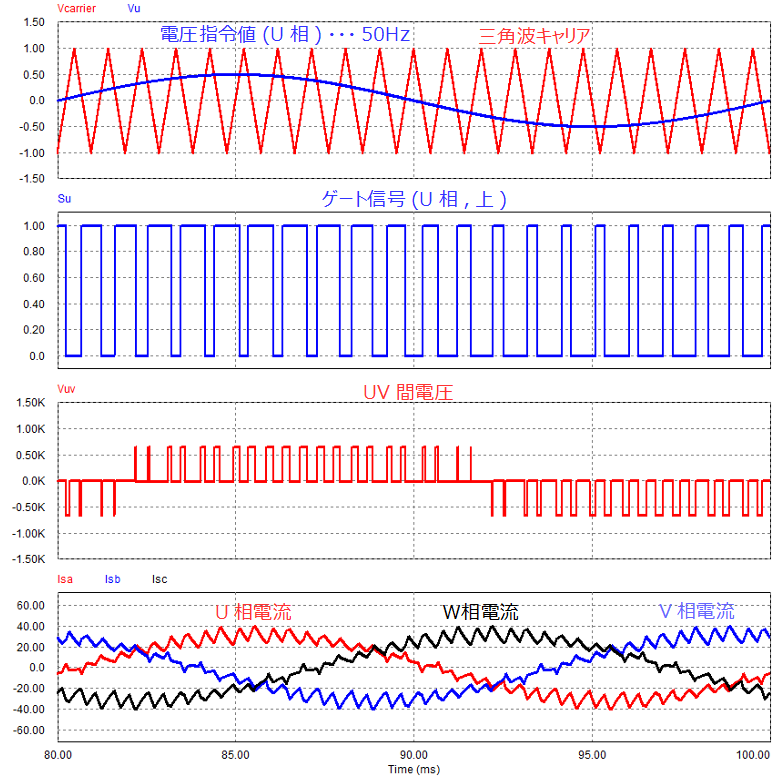
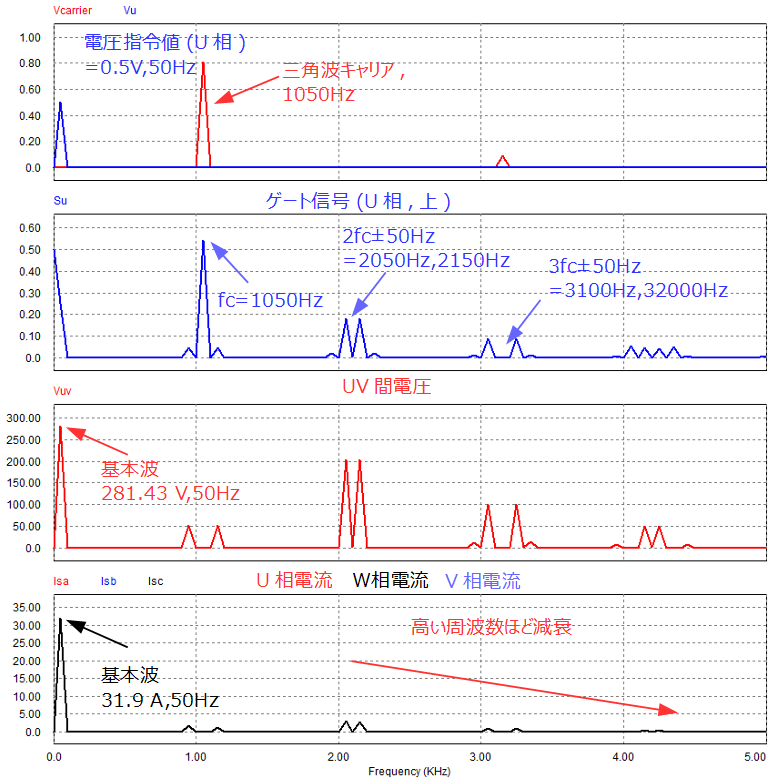
この条件で制御した波形および各波形のFFT結果は下図のようになります。
直流電圧\(V_{dc}\)は650Vとしていますので、出力電圧(線間電圧)\(V_o\)は
\[V_o=\frac{V_{dc}}{2}*a*\sqrt{3}=281.4V\]
となります。
また、この時の相電流\(I_u、I_v、I_w\)の振幅は
\[Iu = \frac{V_o}{\sqrt{3}}*\frac{1}{\sqrt{R^2+{ωL}^2}}=31.9A\]
となります。
FFT結果からも同様の結果となっていることが確認できます。
また、相電流の高調波成分に着目すると周波数が高くなるにつれて、成分が小さくなっています。
これは負荷としてRL負荷を接続しており、RL負荷が一次遅れ要素として働くためです。これにより、高周波ほど減衰が大きく効く(周波数特性におけるゲインが小さい)ためです。
一次遅れ要素と各周波数における減衰(ゲイン)については以前の記事を参考にしてください。

過変調

概要

前章のPWM方式の解説では変調率が1.0以下を対象としていました。
この場合、出力可能な最大電圧は
\[V_o=\frac{V_{dc}}{2}\sqrt{\frac{3}{2}}\]
となります。
さらに電圧を出力したい場合は変調率を1.0よりも大きくする必要があります。
つまり、三角波キャリアのピーク値＜電圧指令値のピーク値となります。
このように変調率が1.0以上の変調方法を過変調といいます。

動作波形

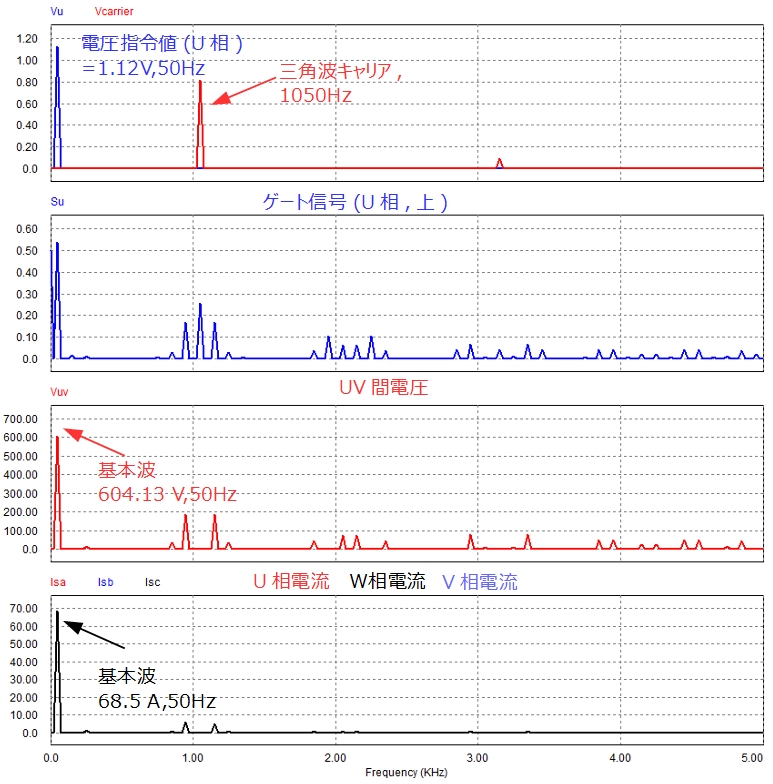
過変調での動作確認として電圧指令値のピーク値1.12Vの場合の波形を以下に示します。
この時、ゲート信号を見てみると電圧指令値のピーク付近でスイッチングしていない(この区間は常に電圧指令値＞三角波キャリアとなるため)ことが確認できます。
また、FFT波形から線間電圧波形のピーク値が604.13Vになっています。
電圧指令値のピーク値が1.12V(変調率M=1.12)であるため、理論的には、
\[V_o=\frac{V_{dc}}{2}*a*\sqrt{3}=\frac{650}{2}*1.12*\sqrt{3}=630.46V\]
出力されるはずですが、4.2%程度小さい値となっています。

三次調波重畳とは

概要

前章で示したように過変調を利用することによって、出力電圧を増加させることができる反面、指令値通りに出力電圧を制御できないといったデメリットがありました。
これは電圧指令値のピークが三角波キャリアの大きさを超えることでスイッチングできない区間が存在することが原因として挙げられます。
そのため、何かしらの方法で、電圧指令値のピークを下げることができれば、上記の問題は解決して、出力電圧を増加させることが可能になります。
本章ではその方法の一つである三次調波重畳方式について解説します。
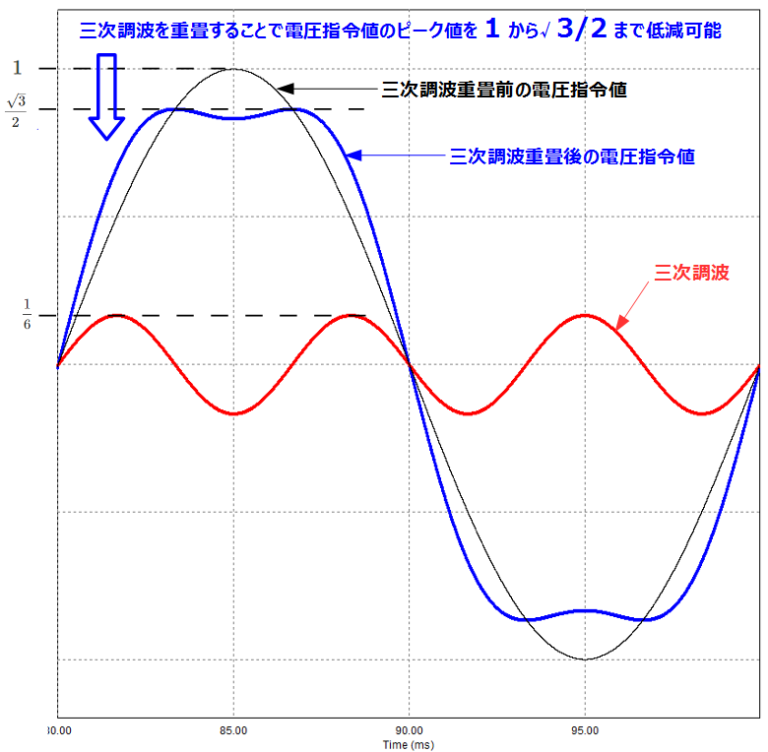
これは下図のように電圧指令値の基本波に対して、三倍の周波数の正弦波を加算することによりピークを抑えた電圧指令値を生成するといったものです。これにより、通常の過変調ではスイッチングしていなかった区間もスイッチングができるようになります。
U、V、Wの各相に三次調波を重畳してはいますが、線間電圧では各相の三次調波がキャンセルされるため、線間電圧の歪を増大させずに出力電圧を増加させられるメリットがあります。

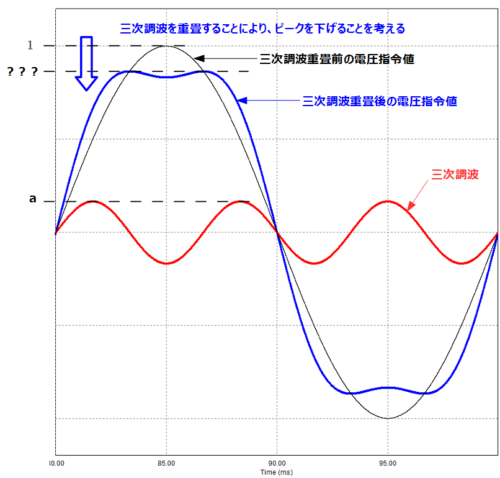
上図は電圧指令値として、ピーク値:1の正弦波に対して、ピーク値:aの三次調波を重畳した場合の波形を示しています。
この時、三次調波のピーク値:\(a\)をどのように設定すれば、効果的に電圧指令値のピーク値を下げられるか考えてみましょう。

最適な三次調波の導出

三次調波重畳後の電圧指令値を\(V_uRef\)とすると、
\[V_uRef = \sinθ+a\sin3θ・・・(☆1)\]
となります。\(V_uRef\)の最大値が三角波キャリアのピーク値(\(1.0\))を越えなければ、全領域でスイッチングすることが可能となります。
そのため、以降の説明では2ステップで導出を行っていきます。
<STEP1>
　(☆1)を\(θ\)で偏微分することで\(V_uRef\)が最大値をとるときの\(θ\)を求める
<STEP2>
　\(V_uRef\)の最大値が最も小さくなる三次調波のピーク値\(a\)を求める
<STEP3>
　<STEP1>、<STEP2>の結果を基にどの程度の電圧まで三次調波重畳によって出力可能かを求める

<STEP1>
\[\frac{\partial}{\partial θ}V_uRef
\\=\cosθ+3a\cos3θ
\\=\cosθ+3a(4\cos^3θ-3\cosθ)
\\=\cosθ(1+12a\cos^2θ-9a)=0
\\⇔12a\cos^2θ=9a-1
\\⇔\cos^2θ=\frac{9a-1}{12a} (・・・\sin^2θ=1-\cos^2θ=\frac{3a+1}{12a})・・・(☆2)\]
これが、\(V_uRef\)が最大値の時の\(θ\)の条件です。

<STEP2>
次に\(V_uRef\)の最大値を求めてみます。
\[V_uRef
\\= \sinθ+a\sin3θ
\\=\sinθ+a(-4\sin^3θ+3\sinθ)
\\=\sinθ(1+3a-4\sin^2θ)\]
となるので、(☆2)を用いると、
\[V_uRef
\\=\sqrt{\frac{3a+1}{12a}}\{(3a+1)-4a\frac{3a+1}{12a}\}
\\=\sqrt{\frac{3a+1}{12a}}\{(3a+1)-\frac{3a+1}{3}\}
\\=\frac{2}{3}\sqrt{\frac{3a+1}{12a}}(3a+1)\}
\\=\frac{2}{3\sqrt{12}}\sqrt{27a^2+27a+9+\frac{1}{a}}・・・(☆3)\]
と\(a\)の式になります。
三次調波の重畳により、電圧指令値のピークを極力下げたいため、(☆3)を\(a\)で微分して、\(V_uRef\)を最小化できる\(a\)を求めてみましょう。
\[\frac{dV_uRef}{da}
\\ = \frac{2}{3\sqrt{12}}\frac{1}{2}\frac{54a^3+27a^2-1}{a^2\sqrt{27a^2+27a+9+\frac{1}{a}}}\]
\(\frac{dV_uRef}{da}=0\)となるのは
\[54a^3+27a^2-1=0⇔(6a-1)(3a+1)^2=0⇔a=\frac{1}{6},-\frac{1}{3}\]
\(a\)は三次調波の振幅のため\(a>0\)より\(a=\frac{1}{6}\)となります。

<STEP3>
\(a=\frac{1}{6}\)の時\(θ\)は\(θ=\frac{π}{3}\)となり、\(V_uRef\)のピーク値は
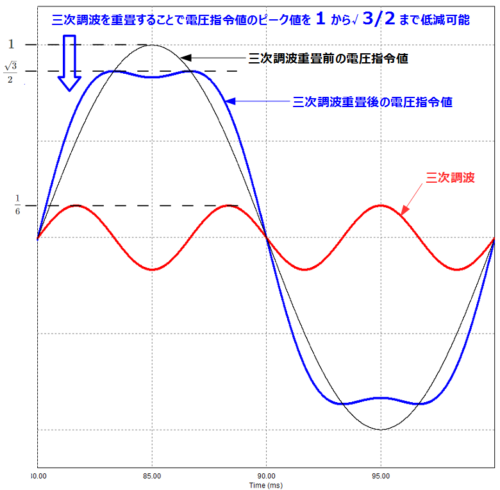
\[V_uRef = \sinθ+a\sin3θ=\sin\frac{π}{3}+\frac{1}{6}\sinπ=\frac{\sqrt{3}}{2}\]
つまり、三次調波重畳を行うことにより、重畳前の電圧指令値のピーク値を\(1⇒\frac{\sqrt{3}}{2}\)まで下げることが可能となります。
言い換えると三次調波重畳しない場合よりも\(\frac{2}{\sqrt{3}}≒1.15\)倍まで出力することができることとなります。

効果検証

ここで、三次調波重畳を行った時の波形を確認してみましょう。
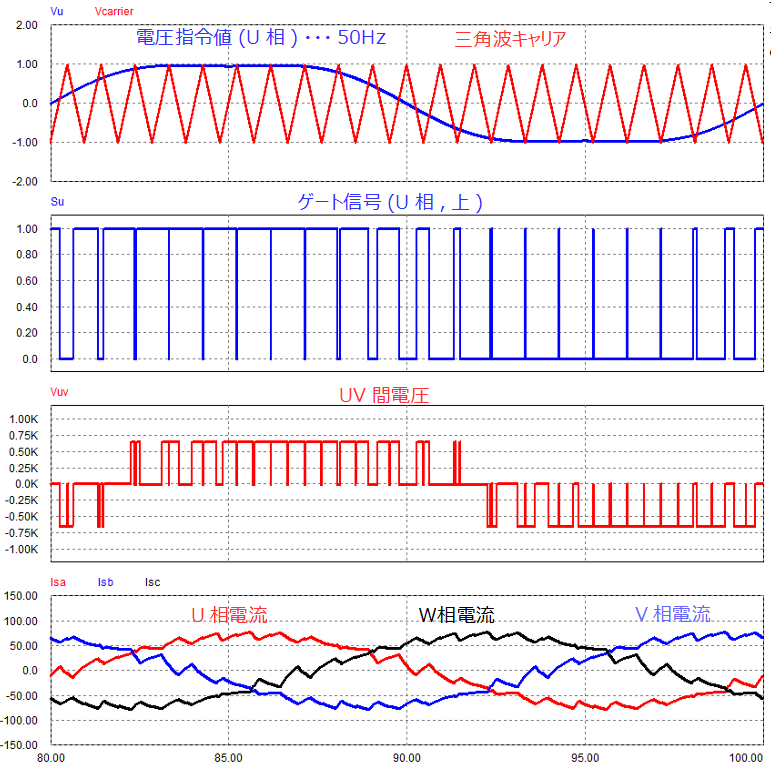
電圧指令値を基本波成分の振幅は前章と同じ1.12Vとして、以下のように与えています。
\[V_u=1.12\sinθ+\frac{1.12}{6}sin3θ\]
前章の波形では電圧指令値のピーク付近でスイッチングしていなかったのに対して、今回は電圧指令値の一周期にわたり、スイッチングしていることが確認できます。
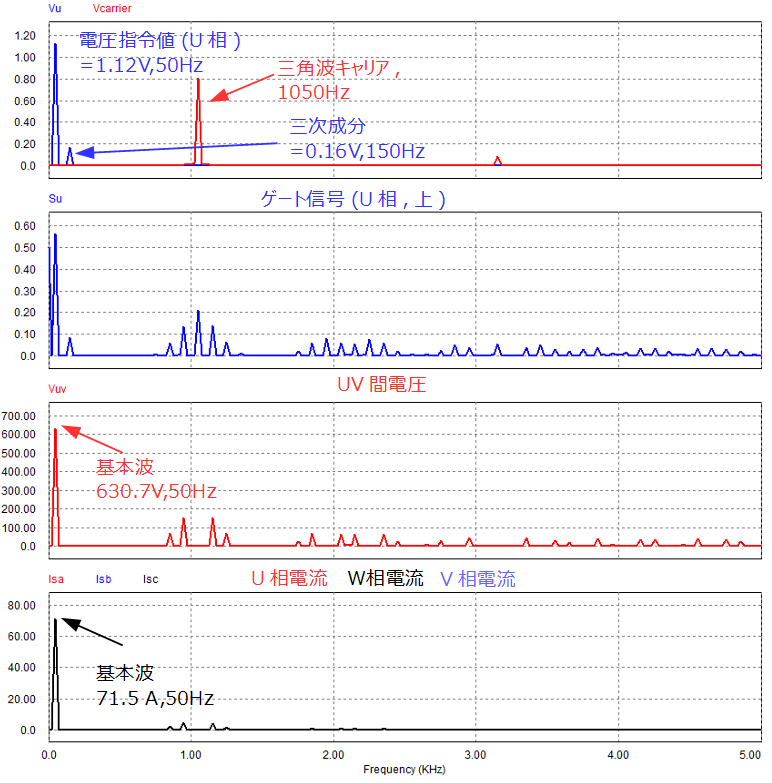
また、FFT波形の線間電圧のピーク値が630.7Vとなっており、ほぼ理論値通りの電圧を出力できています。
また、三次調波重畳を行っているため、電圧指令値には基本波+三次成分が見えていますが線間電圧には三次成分なく、歪の少ない電圧が出力できていることも併せて確認できました。

まとめ

1. 三角波キャリアと電圧指令値の振幅の比率を変調率と呼ぶ、また、変調率が1.0を超えている状態を過変調と呼ぶ
2. 三次調波重畳により過変調でない場合に対して、1.15倍の大きさの電圧まで出力可能
3. 三次調波重畳を行った場合でも線間電圧の歪の増大なし