本記事では伝達関数の概要からRC回路を対象とした伝達関数算出の具体例を示した後、伝達関数の有用性について解説しています。
伝達関数とは
制御系はいくつかの構成要素の結合によって構成されており、システム全体として目標値と制御量の入出力信号を保有しています。ここで制御系の構成要素についても入出力信号があります。それぞれの構成要素は入力信号を出力信号に変えて伝達していることから伝達要素とも呼ばれます。多くの伝達要素は入力信号\(u(t)\)、出力信号\(x(t)\)とすると、以下のような線形微分方程式で記述される入出力信号の伝達関係を与えます。
\[\frac{d^nx}{dt^n}+a1\frac{d^{n-1}x}{dt^{n-1}}+…+a_{n-1}\frac{dx}{dt}+a_nx\\
\quad= b_0\frac{d^mu}{dt^m}+b_1\frac{d^{m-1}u}{dt^{m-1}}+…+b_{m-1}\frac{du}{dt}+b_mx \]
上記の式は入力信号\(u(t)\)が与えられたとき、どのような出力信号\(x(t)\)を発生するかその特性を示した数式モデルを表しています。
ただ、この式は入出力関係を表せる一方で、表現が煩雑であるため、これを簡略化かつ制御系の解析や設計を容易にするために伝達関数を導入します。
伝達関数とは初期条件をすべて零にとしたときの出力のラプラス変換と入力のラプラス変換の比として、以下のように定義づけられます。
\[\color{red} {伝達関数=\frac{出力のラプラス変換}{入力のラプラス変換}}\]
\[ (s^n + a_1s^{n-1}+ a_2s^{n-2}+…+a_{n-1}s+a_n)X(s)\\
\quad = (b_0s^m + b_1s^{m-1}+ b_2s^{m-2}+…+b_{m-1}s+b_m)U(s)\]
\[\frac{X(s)}{U(s)} = \frac{b_0s^m + b_1s^{m-1}+ b_2s^{m-2}+…+b_{m-1}s+b_m}{s^n + a_1s^{n-1}+ a_2s^{n-2}+…+a_{n-1}s+a_n}\]
ここで、\(X(s)/U(s)\)を\(G(s)\)として表記すると
\[X(s) = G(s)U(s)\]
となる。つまり出力のラプラス変換は入力のラプラス変換と伝達関数の積によって求めることができます。
伝達関数計算の具体例(RC回路)
伝達関数計算の具体例として、以下のようなRC回路を考えてみます。入力電圧を\(v_i\)、出力電圧を\(v_o\)として以下の3ステップで伝達関数を計算できます。

【1】まず、回路方程式は以下のようになります。
\[v_i = Ri + v_o \]
\[v_o = \frac{1}{C}\int i dt \]
【2】【1】の2式をラプラス変換します。
\[V_i = RI + V_o\]
\[V_o = \frac{1}{Cs}I ⇔ I = sCV_o\]
【3】【2】の2式からIを消去して、出力/入力の形になるようにして、伝達関数G(s)を算出します。
\[ \ G(s) = \frac{V_o}{V_i} = \frac{1}{1 + sRC}\]
ここで、入力電圧として振幅=\(V_{amp}\)のステップ入力を加えたと考えると出力電圧は伝達関数を用いて以下のように計算できます。
\[ \ V_o = G(s) * V_i = \frac{1}{1 + sRC} * \frac{V_{amp}}{s}\]
これを逆ラプラス変換を用いて、出力電圧の時間応答を求めると以下のようになります。
(※ラプラス変換、逆ラプラス変換についてはこちらの記事を参照ください)
\[v_o = V_{amp}(1-e^{-\frac{1}{RC}t})\]
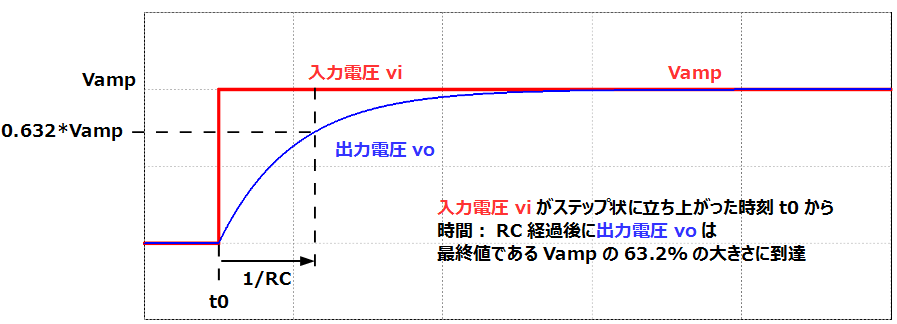
上式より時間が十分に経った最終値は\(V_{amp}\)となります。また、ステップ入力から時間:RC経過時の式は以下のようになります。
\[v_o = V_{amp}(1-e^{-\frac{1}{RC}RC})=V_{amp}(1-e^{-1})=0.632V_{amp}\]
波形としては下図のような特性を示します。
出力電圧が最終値の63.2%に到達していることが分かります。
このようにシステムが最終値の63.2%に到達するまでの時間を時定数と呼び、応答速度の指標としてしばしば用いられます。
伝達関数の有用性について
以上のようにRC回路に対して入力電圧をステップ上に印加すると、出力電圧はある時間遅れをもって入力電圧と同様の値に収束していきます。
このように伝達関数\(G(s)\)が以下の形になる要素を一次遅れ要素といいます。
\[ \ G(s) = \frac{K}{1 + Ts}\]
つまり、伝達関数を算出することによってその要素の特性を把握することが可能となります。
以上が伝達関数の概要、RC回路を用いた具体例、伝達関数を用いる利点についての解説となります。
お疲れさまでした!

コメント