本記事では以下を解説しています。
□二次遅れ要素の概要およびそのステップ応答の導出方法
□逆ラプラス変換する際の部分分数展開をヘビサイドの展開定理を用いて簡略化する手法
□ヘビサイドの展開定理を適用する対象の数式に重解が含まれる場合の計算手法
□RLC回路を対象にした二次遅れ要素の具体例の紹介、解析方法
□二次遅れ要素の応答を決定する二要素(減衰定数、固有角周波数)を変更した場合の影響
二次遅れ要素の概要
基本式
以下の式の伝達関数で表される要素を二次遅れ要素とよばれます。\(ζ\)は減衰定数、\(ω_n\)は固有角周波数とよばれます。
\[G(s) = \frac{{ω_n}^{2}}{s^{2} + 2ζω_ns + {ω_n}^{2}} ・・・(☆)\]
ステップ応答
制御工学の分野でしばしば使用されるステップ応答の導出について以下に示します。
入力として振幅\(E\)のステップ入力\(V_i\)を入力した場合の応答\(V_o\)を考えてみましょう。
\[V_i = \frac{E}{s}・・・(1)\\
V_o =G(s)・V_i = \frac{{ω_n}^{2}}{s^{2} + 2ζω_ns + {ω_n}^{2}} ・\frac{E}{s}・・・(2)\]
上式を逆ラプラス変換することにより、\(v_o\)の応答を求めることができますが、分母の
\[ s^{2} + 2ζω_ns + {ω_n}^{2} = 0・・・(3)\]
の解によって場合分けが必要になります。上式の判別式は
\[4{ω_n}^{2}(ζ^{2}-1)・・・(4)\]
となるため、以下の3通りで場合分けが行えます。
- \(ζ=1\)・・・重解をもつ
- \(ζ>1\)・・・異なる2つの実数解をもつ
- \(ζ<1\)・・・異なる2つの虚数解をもつ
\(ζ=1\)の場合
まずは、1. の\(ζ=1\)の場合について考えます。\(V_o\)は以下の式になります。
\[ V_o = \frac{{ω_n}^{2}}{s^{2} + 2ω_ns + {ω_n}^{2}} ・\frac{E}{s} \\=\frac{{ω_n}^{2}}{(s+ω_n)^{2}} ・\frac{E}{s}・・・(4)\\※重解はs=-ω_n\]
よって、これを部分分数展開すると以下のようになります。
\[ \ V_o = \frac{k_1}{s} + \frac{k_{21}}{(s-ω_n)^{2}}+ \frac{k_{22}}{s-ω_n}・・・(5) \]
ここで、上式の定数\(k_1、k_{21}、k_{22}\)は係数比較によって求めることもできますが、以下に示すヘビサイドの展開定理を用いて算出することもできます。
本記事では以下のヘビサイドの展開定理を用いて\(k_1、k_{21}、k_{22}\)を求めています。
【ヘビサイドの展開定理】
この時、上式の分子の定数\(k_i\)は以下のように求めることができる
\[k_i = \lim_{s \to p_i}(s-p_i)F(s)・・・(★)\]
※詳細はこちらの章に示しています。
\[k_1 = \lim_{s \to 0}sV_o = \lim_{s \to 0}s\frac{{ω_n}^{2}}{(s+ω_n)^{2}} ・\frac{E}{s}= \lim_{s \to 0}\frac{{ω_n}^{2}}{(s+ω_n)^{2}}・E\\
= E\]
\(k_{21}\)も同様に、
\[k_{21} = \lim_{s \to -ω_n}(s+ω_n)^2 V_o = \lim_{s \to -ω_n}\frac{{ω_n}^{2}}{s}E\\
= -Eω_n\]
\(k_{21}\)も同じ要領で求めたいところですが、以下のようにゼロ除算が発生してしまいます。
\[k_{22} = \lim_{s \to -ω_n}(s+ω_n) V_o = \lim_{s \to -ω_n}\frac{{ω_n}^{2}}{(s+ω_n)s}E\]
そのため、重解をもつ場合には以下のように一工夫して定数を求める必要があります。
【重解を含む場合のヘビサイドの展開定理】
まず、(4)を部分分数展開した結果が(5)であるため、(4)=(5)として、さらに\(k_{21}\)を求めるために\(V_o\)に\((s+ω_n)^2\)を掛けた場合を考えます。
\[\frac{{ω_n}^{2}}{(s+ω_n)^{2}} \frac{E}{s} = \frac{k_1}{s} + \frac{k_{21}}{(s+ω_n)^{2}}+ \frac{k_{22}}{s+ω_n}\\
↓ 両辺に(s+ω_n)^2を掛ける\\ E\frac{{ω_n}^{2}}{s} = \frac{k_1(s+ω_n)^{2}}{s} + k_{21}+ k_{22}(s+ω_n) \]
これを両辺微分して\(s=-ω_n\)を代入すると求めたい定数\(k_{22}\)のみが残ることになります。
\[\frac{d}{ds}(E\frac{{ω_n}^{2}}{s}) = \frac{d}{ds}(\frac{k_1(s+ω_n)^{2}}{s} + k_{21}+ k_{22}(s+ω_n))\\
⇔ -E\frac{{ω_n}^{2}}{s^2} = \frac{k_1(2(s+ω_n)-(s+ω_n)^2)}{s^2} + k_{22} \\
↓ 両辺にs=-ω_nを代入\\
k_{22} = -E
\]
よって、(5)式は以下のようになり、
\[V_o = E(\frac{1}{s} – \frac{ω_n}{(s-ω_n)^{2}} – \frac{1}{s-ω_n})・・・(6) \]
これを逆ラプラス変換すると以下(7)式のように時間応答\(v_o\)が求められます。
\[v_o = E(1-e^{-ω_nt}(1+ω_nt))・・・(7)\]
※ラプラス変換、逆ラプラス変換の概要や変換表についてはこちらの記事をご覧ください。
\(ζ≠1\)の場合
2. と3.の\(ζ≠1\)の場合も同様に考えていきます。
まず、(3)式の解は以下のようになります。
\[s = -ζω_n±ω_n\sqrt{ζ^2 – 1}\]
それぞれ、以下のように\(p_1、p_2\)と置いて、\(V_o\)を部分分数展開すると以下のようになります。
\[p_1 = -ζω_n-ω_n\sqrt{ζ^2 – 1}、p_2 = -ζω_n+ω_n\sqrt{ζ^2 – 1} ※ζ>1・・・(8)\\
p_1 = -ζω_n-jω_n\sqrt{1-ζ^2}、p_2 = -ζω_n+jω_n\sqrt{1 – ζ^2} ※ζ<1・・・(9)\]
\[ V_o = \frac{{ω_n}^{2}}{s^{2} + 2ω_ns + {ω_n}^{2}}\frac{E}{s} \\
\quad= \frac{E{ω_n}^{2}}{s(s-p_1)(s-p_2)}\\
\quad= \frac{k_1}{s} + \frac{k_2}{s-p_1}+ \frac{k_3}{s-p_2}・・・(10)\]
\(ζ=1\)の場合と同様にヘビサイドの展開定理を用いて、各定数を求めると以下のようになります。
\[k_1 = E\\
k_2 = \frac{E{ω_n}^{2}}{p_1(p_1-p_2)}\\
k_3 = \frac{E{ω_n}^{2}}{p_2(p_2-p_1)}\]
これより、(10)式の逆ラプラス変換を求めると(11)式のように時間応答\(v_o\)を求めることができます。
\[v_o = k_1 + k_2 e^{p_1t} + k_3 e^{p_2t}・・・(11) \]
ここから、さらに1. \(ζ>1\)の場合 と 2.\(ζ<1\)の場合 について詳しく調べてみます。
<\(ζ>1\)の場合>
\(p_1、p_2\)は(8)式のようになるため
\[k_2 = \frac{E{ω_n}^{2}}{p_1(p_1-p_2)} =E\frac{p_2}{p_1-p_2} = E\frac{ζ+\sqrt{ζ^2 – 1}}{2\sqrt{ζ^2 – 1}} \\
k_3 = \frac{E{ω_n}^{2}}{p_2(p_2-p_1)} =E\frac{p_1}{p_2-p_1} = E\frac{ζ-\sqrt{ζ^2 – 1}}{2\sqrt{ζ^2 – 1}} \]
(11)式の時間応答は以下(12)式のようになります。
\[v_o = E(1 – \frac{e^{-ζω_nt}}{2\sqrt{ζ^2 – 1}}\{(ζ+\sqrt{ζ^2 – 1})e^{ω_n\sqrt{ζ^2 – 1}t} – (ζ-\sqrt{ζ^2 – 1})e^{-ω_n\sqrt{ζ^2 – 1}t}\}・・・(12)\]
<\(ζ<1\)の場合>
\(p_1、p_2\)は(9)式のようになるため
\[k_2 = -\frac{E}{2j}・\frac{ζ+\sqrt{1 – ζ^2}}{\sqrt{1 – ζ^2}} \\
k_3 = \frac{E}{2j}・\frac{ζ-\sqrt{1 – ζ^2}}{\sqrt{1 – ζ^2}} \]
(11)式の時間応答は以下(13)式のようになります。
\[v_o = E(1 – \frac{e^{-ζω_nt}}{\sqrt{1 – ζ^2}}\sin(\sqrt{1 – ζ^2}ω_nt + \tan^{-1}(\frac{\sqrt{1 – ζ^2}}{ζ}))・・・(13)\]
ヘビサイドの展開定理
以下の有理関数F(s)について
\[F(s) = \frac{b_0s^m + b_1s^{m-1}+ b_2s^{m-2}+…+b_{m-1}s+b_m}{a_0 s^n + a_1s^{n-1}+ a_2s^{n-2}+…+a_{n-1}s+a_n}・・・(b1)\]
分母多項式
\[a_0 s^n + a_1s^{n-1}+ a_2s^{n-2}+…+a_{n-1}s+a_n = 0・・・(b2) \]
の解を\(p_1、p_2、p_3、・・・、p_n\)とする時、F(s)は以下のように部分分数に展開できる
\[F(s) = \frac{k_1}{s-p_1}+\frac{k_2}{s-p_2}+\frac{k_3}{s-p_3}+\frac{k_n}{s-p_n}・・・(b3)\]
【ヘビサイドの展開定理】
この時、上式の分子の定数\(k_i\)は以下のように求めることができる
\[k_i = \lim_{s \to p_i}(s-p_i)F(s)・・・(★)\]
<導出>
(★)は次のように導かれる。F(s)は(b3)のように展開されるから両辺に\(s-p_i\)を掛けると
\[(s-p_i)F(s) = \sum_{j=1}^n \frac{s-p_i}{s-p_j}k_j + \frac{s-p_i}{s-p_i}k_i \]
となる。ここで、両辺のsを\(p_i\)に近づければ、以下の式の通り、右辺の\(k_i\)以外の項は0に漸近する。
\[\lim_{s \to p_i}(s-p_i)F(s) = \lim_{s \to p_i} \sum_{j=1}^n \frac{s-p_i}{s-p_j}k_j + k_i \]
以上のように(★)が導かれる
具体例(RLC回路)
以下の図に示すRLC回路を対象に2次遅れ要素のステップ応答の解析を行ってみます。
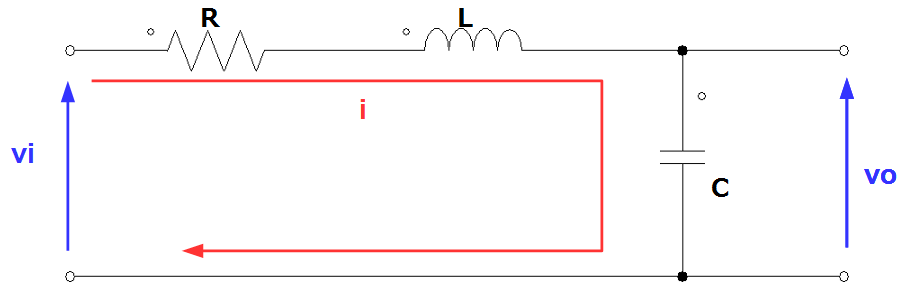
まず、回路方程式は以下のようになります。
\[v_i – v_o = Ri + L \frac{d}{dt}i \\ i = C \frac{d}{dt}v_o \]
上式から\(i\)を消去すると以下のようになります。
\[v_i – v_o = RC\frac{d}{dt}v_o + LC \frac{d^{2}}{dt^{2}}v_o \]
これを初期値ゼロとしてラプラス変換すると以下のようになります。
\[V_i = (LC s^{2} + RC s + 1)V_o \]
この時、伝達関数G(s)は以下のようになります。
\[G(s) = \frac{1}{LC s^{2} + RC s + 1} = \frac{\frac{1}{LC}}{s^{2} + R/L s + \frac{1}{LC}} \\
\quad=\frac{(\sqrt{\frac{1}{LC}})^{2}}{s^{2} + 2 \frac{RC}{2 \sqrt{LC}} \sqrt{\frac{1}{LC}} s + (\sqrt{\frac{1}{LC}})^{2}}\]
上式において、\(ζ = \frac{RC}{2 \sqrt{LC}},ω_n = \sqrt{\frac{1}{LC}}\)とすると(☆)の二次遅れ要素の式と等価になります。
そのため、入力電圧\(v_i\)をステップ状に変化させた場合の出力電圧\(v_o\)の時間応答(ステップ応答)は\(ζ\)の値によって(7)、(12)、(13)式のようになります。
最後に\(ζ\)と\(ω_n\)を変化させた場合の特性を確認してみましょう。
減衰定数\(ζ\)が変わった場合の特性
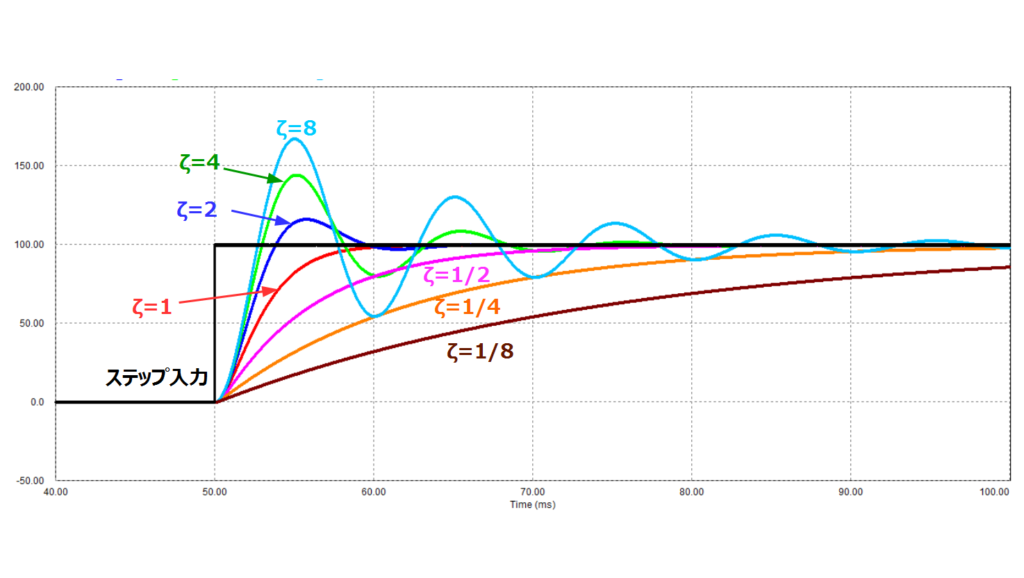
シミュレーション回路中の\(R\)の値を変更して\(ζ\)が変わるようにしてシミュレーションを行った結果を以下に示します。
なお、\(ζ\)を変動させた場合も\(ω_n\)が変わらないように\(R\)のみ変更としています。
※\(ζ = \frac{RC}{2 \sqrt{LC}},ω_n = \sqrt{\frac{1}{LC}}\)のため、\(R\)のみ変更すれば\(ω_n\)を変えず、\(ζ\)を変えられます。
波形を見ると\(ζ\)の範囲によって以下のように特性が変化します。
- \(ζ=1\)・・・出力は定常値に単調に接近、立ち上がりも緩やかです。
この状態を過制動といいます - \(ζ>1\)・・・振動が生じない限界、この値を超えると振動的な波形になります。
この状態を臨界制動とよばれます - \(ζ<1\)・・・振動的になり定常値になるのに時間を要します。
この状態を不足制動とよびます。
このように減衰定数\(ζ\)は過渡応答の減衰の度合いに関係していることがわかります。
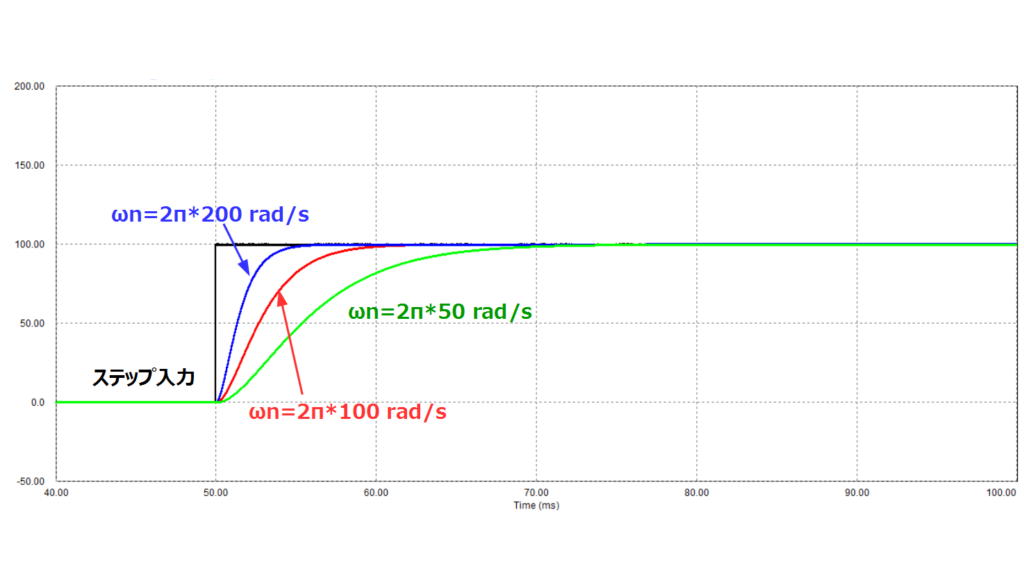
固有角周波数\(ω_n\)が変わった場合の特性
シミュレーション回路中の\(R、L、C\)の値を変更して\(ω_n\)が変わるようにしてシミュレーションを行った結果を以下に示します。
なお、\(ω_n\)を変動させた場合も、常に以下のように\(ζ=1\)となるように\(R、L、C\)の値を変更しています。
\(ω_n = 2π・100 rad/s\)の場合 ⇒ \(R = 1.25 Ω、L = 1 mH、C = 2533μF\)
\(ω_n = 2π・200 rad/s\)の場合 ⇒ \(R = 2.5 Ω、L = 1 mH、C = 633μF\)
\(ω_n\)を大きくするにつれ、最終値に到達する時間が短くなっていることがわかります。
このように固有角周波数\(ω_n\)は応答の速さの尺度を与えていることになります。
以上が二次遅れ要素の概要およびそのステップ応答の導出方法と計算を便利にするためのヘビサイドの展開定理の使用方法の解説、ヘビサイドの展開定理を使用する際に重解をもつ場合の解法とRLC回路を対象にした具体例の説明と二次遅れ要素の特性を決める二要素(減衰定数と固有角周波数)が変動した場合の影響についての解説になります。
お疲れさまでした!



コメント