制御工学の基礎~ボード線図はどう描くのか？書き方のテクニック解説~

本記事では制御工学の周波数応答解析に頻繁に利用されるボード線図の書き方、代表的な制御要素のボード線図の解説を行った後、複雑な伝達関数を対象としたボード線図を作図するためのテクニックを解説しています。

ボード線図の書き方
1. ボード線図とは
2. ボード線図の書き方(一次遅れ要素)
代表的なボード線図
1. 微分要素/積分要素
一次遅れ要素
ボード線図の重ね合わせ
1. 概要
2. 例題
まとめ

ボード線図の書き方

ボード線図とは

ボード線図は伝達関数の周波数特性を表現するツールの一つであり、以下のような特徴があります。

角周波数\(ω\)に対するゲインの変化を示すゲイン曲線と\(ω\)に対する位相差を示す位相曲線の2つの曲線で表現される
ゲイン曲線は横軸に周波数を対数目盛、縦軸にゲイン\(|G(jω)|\)をデシベル(dB)値で表す
位相曲線は横軸に周波数を対数目盛、縦軸に位相差\(\angle G(jω)\)を度(°)の単位で表す

ボード線図の書き方(一次遅れ要素)

一次遅れ要素を対象として、ボード線図の書き方を解説します。
まず、伝達関数は
\[G(s)= \frac{1}{1+Ts}\]
よって周波数伝達関数は以下になります。
\[G(jω)= \frac{K}{1+j・ωT}=\frac{K}{1+ω^2T^2}-j・\frac{K・ωT}{1+ω^2T^2}\]
また、ゲインは以下になります。
\[|G(jω)|=\frac{1}{\sqrt{1+ω^2T^2}}\]
ここで、ボード線図を作成する際はゲインをデシベルで表現する必要があります。
デシベルは以下のように定義されます。

デシベル (英語: decibel 記号: dB)は、ある物理量を基準となる量との比の常用対数によって表したものである。音の強さ、音圧レベル、電力比や電気機器の利得等を表すことが多い。（一般化、抽象化して説明すると）「デシベル」というのは音圧、電力、利得など、物理量をレベル表現を用いて表すときに使用される単位である。（なおSIにおいてレベル表現として表される量には次元が与えられておらず、無次元量である。）電気工学や振動・音響工学などの分野で頻用される。
デシベル-Wikipedia

ボード線図を作図する際は以下のようにゲインをデシベル値として計算します。
\[20 \log_{10}{|G(jω)|}\]
つまり、今回の一次遅れ要素の場合、以下のようになります。

\[20 \log_{10}{|G(jω)|} \\= 20 log_{10}{\frac{1}{\sqrt{1+ω^2T^2}}}\\ = -20 \log_{10}{\sqrt{1+ω^2T^2}}\\ = -10\log_{10}{1+ω^2T^2}・・・(☆1)\]

最後に位相差は以下のようになります。
\[\phi = -\tan^{-1}(-ωT)・・・(☆2)\]

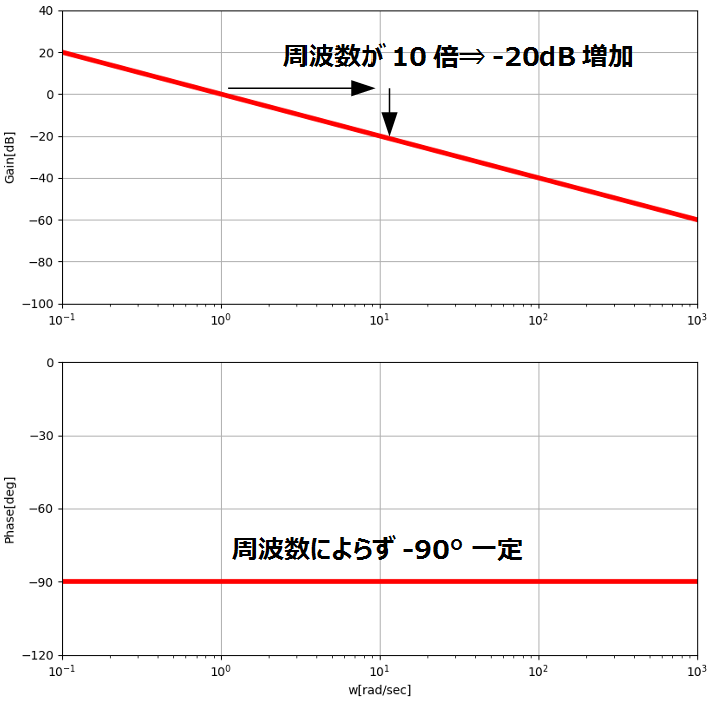
\(ω\)に対する(☆1)、(☆2)の値を表示すると以下のようなボード線図になります。
※下図は(☆1)、(☆2)中で\(T = 1\)とした時のボード線図になります。

代表的なボード線図

微分要素/積分要素

【微分要素】
□伝達関数\[G(s)=s\]
□周波数伝達関数\[G(ω)=j・ω\]
□ゲイン(デシベル)/位相差
\[20 \log_{10}|G(jω)|=20log_{10}ω\\
\phi = 90°\\\]

【積分要素】
□伝達関数\[G(s)=\frac{1}{s}\]
□周波数伝達関数\[G(ω)=\frac{1}{j・ω}=-j・\frac{1}{ω}\]
□ゲイン/位相差
\[20 \log_{10}|G(jω)|=-20log_{10}ω\\
\phi = -90°\]

一次遅れ要素

一次遅れ要素のゲイン、位相は(☆1)、(☆2)の通りです。
ここでは(\T\)の値を変更した場合のゲイン曲線、位相曲線を以下に示します。

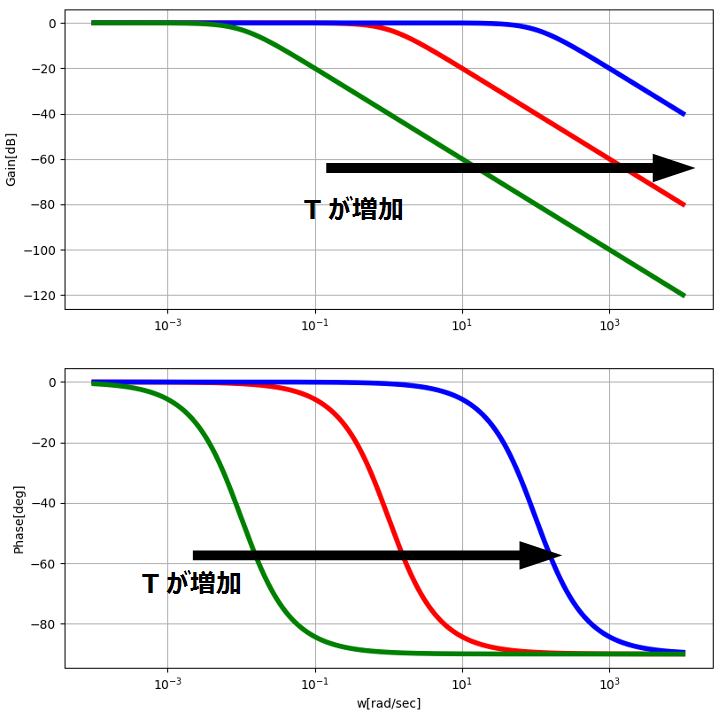
このように(\T\)の値を増加させると、ゲイン曲線、位相曲線ともに右側(高周波側)に平行移動する特性があることが分かります。

ボード線図の重ね合わせ

概要

本章では複雑な伝達関数を対象にしたボード線図の作図方法について解説します。
以下のように複数の周波数伝達関数の積の形で表される\(G(jω)\)について、
\[G(jω)=G_1(jω)・G_2(jω)・G_3(jω)・　・・・　・G_n(jω)\]
\(|G(jω)|\)のデシベル値は
\[20 \log_{10}{|G(jω)|}\\=20 \log_{10}{|G_1(jω)|}・\log_{10}{|G_2(jω)|}・\log_{10}{|G_3(jω)|}・・・・・\log_{10}{|G_n(jω)|}\\
=20 \log_{10}{|G_1(jω)|}+20 \log_{10}{|G_2(jω)|}+20 \log_{10}{|G_3(jω)|}+・・・+20 \log_{10}{|G_n(jω)|}\]
また、位相についても
\[\angle G(jω)=\angle G_1(jω)+\angle G_2(jω)+\angle G_3(jω)+・・・+\angle G_n(jω)\]
となる。
つまり、目的の周波数伝達関数\(G(jω)\)を構成する要素のボード線図を重ね合わせることで、\(G(jω)\)のボード線図を簡単に作図することができます。

ボード線図の重ね合わせ

\(G(jω)\)を構成する各々の要素のゲイン曲線および位相曲線の和が
\(G(jω)\)のゲイン曲線、位相曲線となる

これを具体例を示しながら確認していきます。

例題

以下の伝達関数のボード線図を作図することを考えます。
\[G(s)=\frac{50・(s+2)}{s・(s+10)}\\
↓\\
G(jω)=\frac{50・(jω+2)}{jω・(jω+10)}=・・・\]
↑のように、周波数伝達関数\(G(jω)\)を求めてもボード線図は作図可能ですが、
今回は以下のように要素の積に形に変形する方針で作図してみましょう。
\[G(s)=\frac{50・(s+2)}{s・(s+10)}\\=\frac{100・(0.5s+1)}{10・s・(0.1s+1)}\\=10・\frac{1}{s}・\frac{1}{0.1s+1}・(0.5s+1)\]
ここで、それぞれの要素を以下のように考えます。
\[G_1(s)=10\\G_2(s)=\frac{1}{s}\\G_3(s)=\frac{1}{0.1s+1}\\G_4(s)=0.5s+1\]
すると目的の伝達関数は
\[G(s) = G_1(s)・G_2(s)・G_3(s)・G_4(s)\]
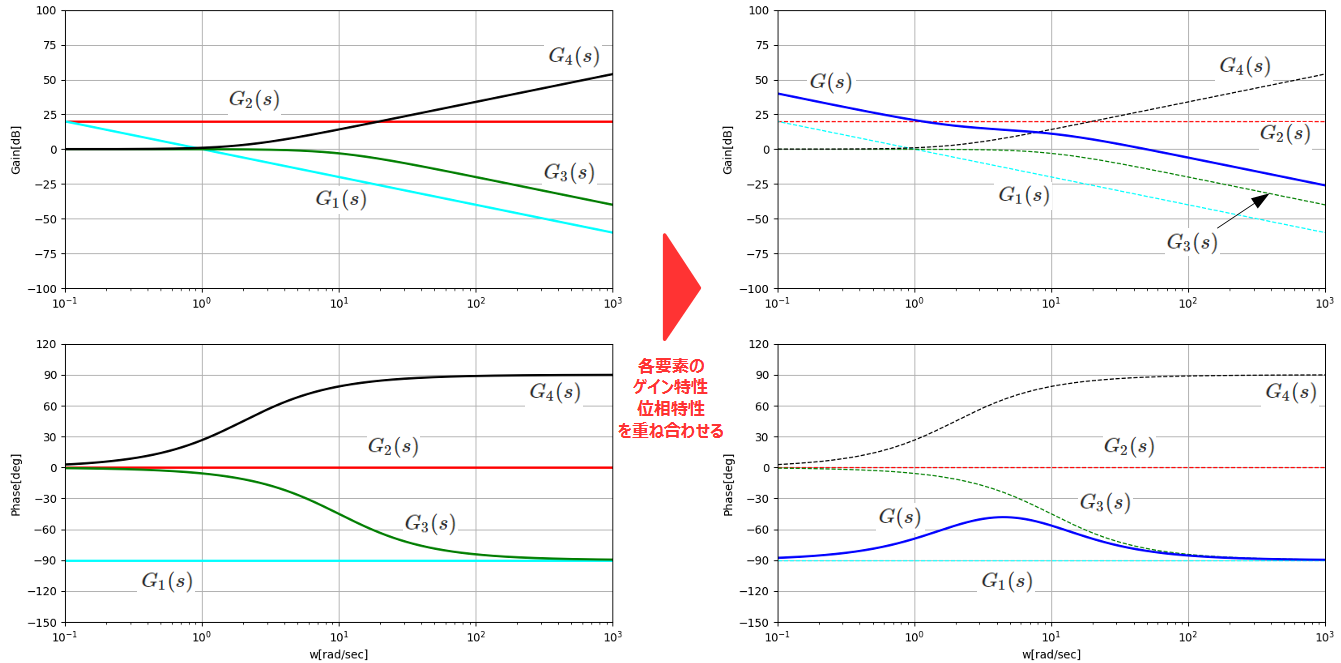
となります。各要素\(G_1(s)~G_4(s)\)は比較的容易にゲイン曲線/位相曲線を作図することができ(左側)、これをボード線図の重ね合わせを用いることで、\(G_1(s)~G_4(s)\)のボード線図を重ねることで\(G(s)\)の伝達関数が求められます(右側)。