本記事ではPMSM制御におけるFF制御の役割と電流制御(FB制御)のゲインの設計方法について、数式/ブロック図を用いて解説しています。
PMSMモデルとFF制御/FB制御
本章では制御系の全体像を捉えるため、PMSMの特性を数式で示したモデルと制御系の構成について示します。
まず、PMSMの電圧方程式は以下のように表されます。
\[
\begin{pmatrix}
V_d \\
V_q
\end{pmatrix}=
\begin{pmatrix}
R_a+pL_d&-ωL_q \\
ωL_d&R_a+pL_q
\end{pmatrix}
\begin{pmatrix}
I_d \\
I_q
\end{pmatrix}+
\begin{pmatrix}
0\\
ωψ_f
\end{pmatrix}・・・①\\
V_d:d軸電圧、V_q:q軸電圧、I_d:d軸電流、I_q:q軸電流、R_a:巻線抵抗、\\
L_d:d軸インダクタンス、L_q:q軸インダクタンス、ψ_f:磁石磁束、\\
ω:電気角周波数、p:微分演算子
\]
これをラプラス変換して、電流\(Id、Iq\)について解くと以下のようになります。
\[ I_d = \frac{1}{R_a+sL_d}\{V_d + ωL_qI_q\}・・・②\\
I_q = \frac{1}{R_a+sL_q}\{V_q + ωL_dI_d+ωψ_f\}・・・③\]
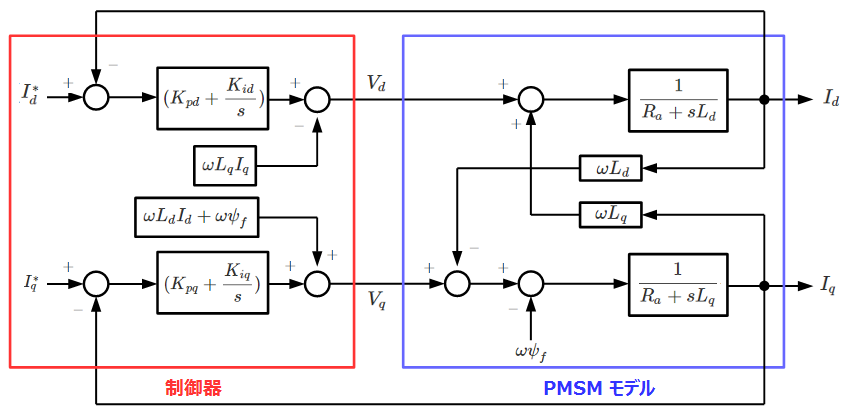
これをブロック図で表すと以下の図のような入力が電圧\(Vd、Vq\)、出力が電流\(Id、Iq\)のモデルとなります。
※以降の解説ではこれをPMSMモデルとして表記しています。
モデル内で\(Id\)の計算に\(Iq\)の項が入ってきたり、\(Iq\)の計算に\(Id\)の項が入ってきたりする部分(下図の赤/青線部分)があり、これを干渉項と呼びます。

このPMSMモデルに制御器から電圧を加えて、所望の電流\(Id,Iq)\)をする場合を考えてみましょう。
以前のフィードバック制御の記事で紹介した通り、FF制御とFB制御を組み合わせて制御を行うこととなります。ここで、FF制御の成分\(V_dFF、V_qFF\)とFB制御の成分\(V_dPI、V_qPI\)はそれぞれ以下の式のようになります。
\[V_dFF = ωL_qI_q・・・④\\
V_qFF = ωL_dI_d+ωψ_f・・・⑤\\
V_dPI = (K_{pd}+\frac{K_{id}}{s})(I_d^*-I_d)・・・⑥\\
V_qPI = (K_{pq}+\frac{K_{iq}}{s})(I_q^*-I_q)・・・⑦\\
※I_d^*:d軸電流指令値、I_q^*:q軸電流指令値\]
これを先程のPMSMモデルの中に制御部として追記すると以下のようなブロック図になります。
FF制御の役割
制御器を構成する主な要素、FF制御/FB制御の内、PMSM制御におけるFF制御の役割について解説していきます。
前章で述べたようにPMSMモデルにはdq軸それぞれ干渉項があります。
干渉項があることにより、d軸入力電圧をd軸電流偏差\(I_d^*-I_d\)から定めたとしても、q軸電流の変動によって、d軸にも影響が及ぼされることとなります。
これに対して、④、⑤式で与えられる電圧をFF制御として予め制御器に与えておくことにより、干渉項を打ち消すことができます。
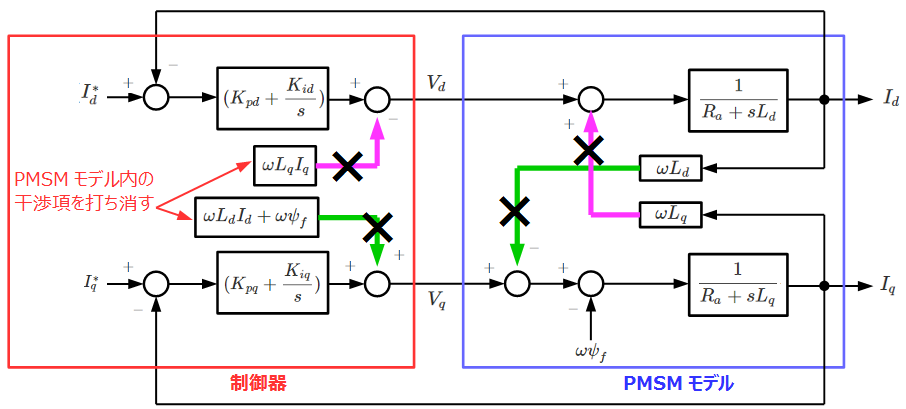
FF制御を入れた場合のブロック図は以下のようになります。dq軸それぞれの入力電圧が出力のdq軸電流と一対一で対応していることが分かります。
このように干渉項を消すように制御項を考えることを非干渉化と呼びます。

FF制御を入れることによりdq軸それぞれ、他方の軸の影響を受けず、独立に制御することが可能になります。
またこのような操作を非干渉化と呼びます。
FB制御ゲインの設計方法
続いて、FB制御ゲインの設計方法です。
下図のブロック図と併せてご確認ください。
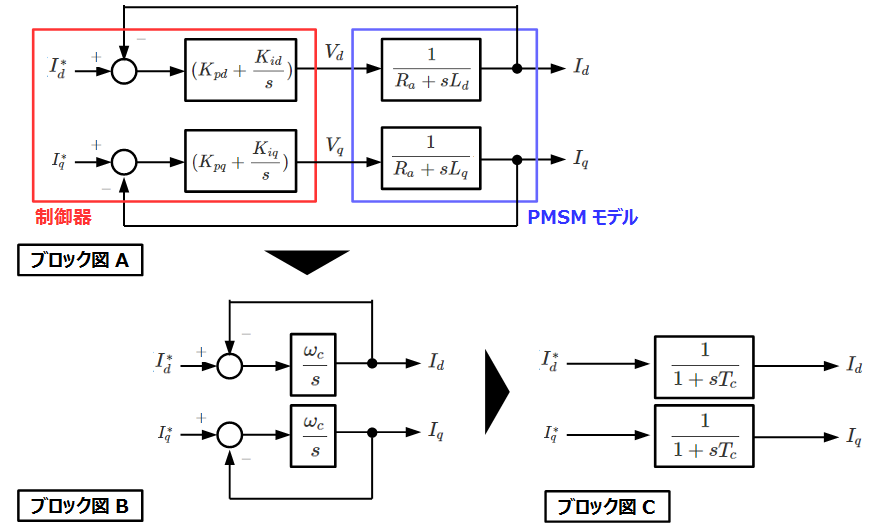
まず、前章でFF制御により非干渉化を行った場合のdq軸の式は以下のようになります(下図、ブロック図A)。
\[I_d = \frac{1}{R_a+sL_d}・\frac{sK_{pd}+K_{id}}{s}(I_d^*-I_d)\\=\frac{1}{L_d(s+\frac{R_a}{L_d})}・\frac{K_{pd}(s+\frac{K_{id}}{K_{pd}})}{s}(I_d^*-I_d)・・・⑧\\
I_q = \frac{1}{R_a+sL_q}・\frac{sK_{pq}+K_{iq}}{s}(I_q^*-I_q)\\=\frac{1}{L_q(s+\frac{R_a}{L_q})}・\frac{K_{pq}(s+\frac{K_{iq}}{K_{pq}})}{s}(I_q^*-I_q)・・・⑨\]
次に、極と零点が等しくなるように、
(例えば、⑧の場合は\(L_d\)と\(K_{pd}\)、\(s+\frac{K_{id}}{K_{pd}}\)と\(s+\frac{R_a}{L_d}\)がそれぞれ約分できるように)
以下の通り、比例ゲインと積分ゲインを設定します。
※極と零点については以下の用語解説をご覧ください。
\[K_{pd}=ω_cL_q,K_{pq}=ω_cL_d,\\K_{id}=ω_cR_a,K_{iq}=ω_cR_a\]
これにより⑧と⑨式はそれぞれ以下の⑩と⑪式のようになります。
dq軸それぞれの極と零点が互いに打ち消しあっているので、非常にシンプルな形になっています(ブロック図B)。
このような操作を極零相殺と呼びます。
\[I_d = \frac{1}{R_a+sL_d}・\frac{ω_c(R_a+sL_d)}{s}(I_d^*-I_d)\\=\frac{ω_c}{s}(I_d^*-I_d)・・・⑩\\
I_q = \frac{1}{R_a+sL_q}・\frac{ω_c(R_a+sL_q)}{s}(I_q^*-I_q)\\=\frac{ω_c}{s}(I_q^*-I_q)・・・⑪\]
最後にこれを\(Id、Iq\)について解くと最終的に以下のようになります(ブロック図C)。
\[I_d = \frac{1}{1+sT_c}{I_d^*}・・・⑫\\
I_q = \frac{1}{1+sT_c}{I_q^*}・・・⑬\\
※T_c = \frac{1}{ω_c}\]
このように、極零相殺を行うことにより、指令値\(I_d^*I_q^*\)を入力、\(I_d^*I_q^*\)を出力とした一次遅れの形で表すことができます。
これにより、比例ゲイン、積分ゲイン設定の段階でパラメータ\(ω_c\)を任意の値にすることで、電流応答を決定することが可能になります。
【極と零点とは】
次のsの有理関数で表される伝達関数
\[G(s) = \frac{b_0s^m + b_1s^{m-1}+ b_2s^{m-2}+…+b_{m-1}s+b_m}{a_0s^n + a_1s^{n-1}+ a_2s^{n-2}+…+a_{n-1}s+a_n}\]
について分母多項式を零とおいた式
\[a_0s^n + a_1s^{n-1}+ a_2s^{n-2}+…+a_{n-1}s+a_n = 0\]
を特性方程式と呼び、この方程式の根を特性根または\(G(s)\)の極といいます。
また、
\[b_0s^m + b_1s^{m-1}+ b_2s^{m-2}+…+b_{m-1}s+b_m = 0\]
の根を\(G(s)\)の零点といいます。
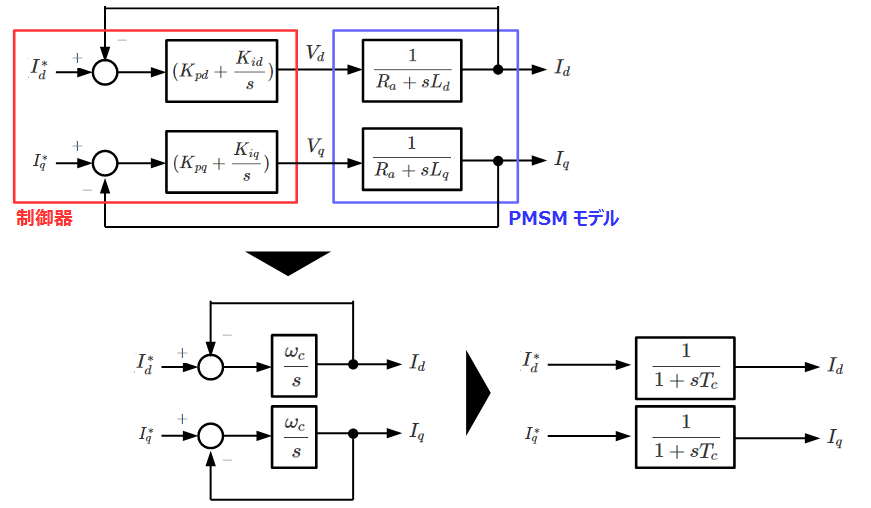
比例ゲイン/積分ゲインはPMSMの巻線抵抗/dq軸インダクタンスに応じて極零相殺できるように設定します。
制御器/モータモデル含めて一次遅れの形となり、応答速度の設計がしやすくなります。
まとめ
本記事のまとめを以下に示します。
- PMSMモデルにはd軸の変動がq軸へ、また、q軸の変動がd軸へ影響を及ぼし合う成分が存在し、これを干渉項と呼ぶ
- FF制御によりPMSMモデル内の干渉項を消去することができる。
これを非干渉化と呼ぶ。 - モータのパラメータに応じて、極零相殺ができるようにFB制御のゲイン設計を行うことにより応答の設計が容易になる。
おつかれさまでした!


コメント