本記事では非正弦波の解析に有効な手法であるフーリエ級数展開の基本について説明した後、実際に矩形波を対象に実際の解析方法やフーリエ級数展開を利用した波形の再現について解説しています。
非正弦波交流の解析方法
非正弦波交流とは
まずは非正弦波交流の定義からですが 周期関数の中で正弦波でない交流信号 になります。
※周期関数とは、すべてのtに対して次式が成り立つ関数として定義されています。
\(v(t) = v(t+T)\)
Tは周期を表します。つまり、ある時刻tに対して、一周期後の時刻t+Tにおいても同じ値をとる関数であることを示しています。
周期関数として代表的なものには三角関数があり、次式で表される正弦波の周期は2π/ω [s]となります。
\(v(t) = A_m \sin (ωt + φ)\)
非正弦波の例としては鋸波や三角波があり、以下に波形を示します。
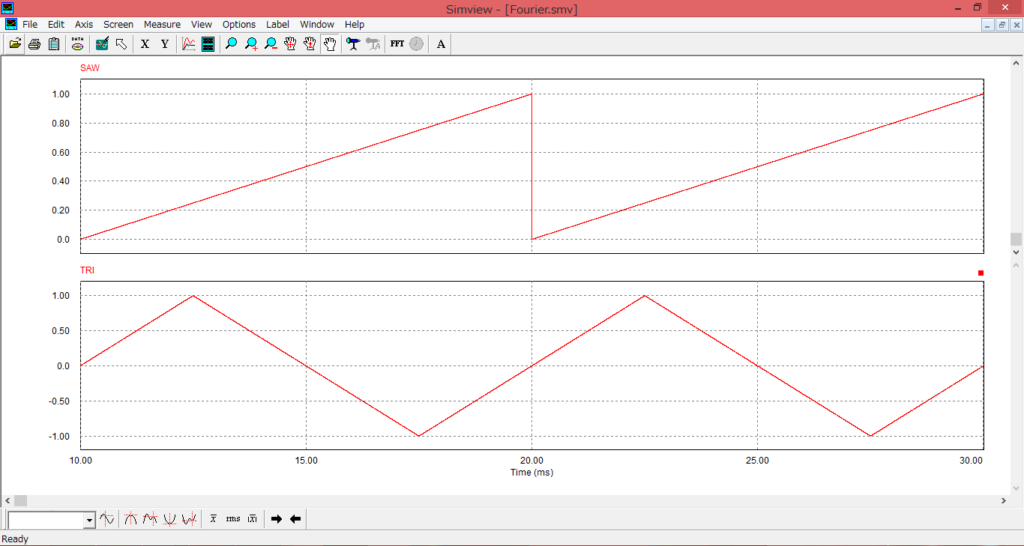
フーリエ級数展開の利用
正弦波であれば上述のように一般的によく知られた数式として表すことができるため、比較的解析が容易である利点があります。一方で、工学の分野で扱う信号には正弦波でない交流波形を対象にすることも稀ではなく、非正弦波交流に対する解析手法の習得が非常に重要になります。
ここで使用されるのがフーリエ級数展開を利用した解析になります。
フーリエ級数展開とは簡単に表現するとどんな周期性をもった非正弦波交流であっても複数の正弦波の和(重ね合わせ)で表現することが可能である とする考え方になります。
数式で表すと以下のようになります。
\(
v(t) = a_0 + a_1 \cosωt + a_2 \cos2ωt + a_3 \cos3ωt + ・・・\\
\hspace{53pt} b_1 \sinωt + b_2 \sin2ωt + b_3 \sin3ωt + ・・・
\)
(※上記の数式はスクロールできます)
\(
v(t) = a_0 + \sum_{k=1}^\infty {a_k \cos kωt + b_k \sin kωt}
\)
上式の右辺をフーリエ級数と呼び、a0、ak、bkをフーリエ係数と呼びます。
周期関数をフーリエ級数で表すことをフーリエ級数展開といいます。
この時、上式の角周波数ωの波を基本波と呼び、ω=2π/T[rad/s]を基本波角周波数、f=1/Tを基本周波数といいます。
フーリエ級数の求め方
上述の通り、フーリエ級数展開にはフーリエ係数の計算が必須になります。各フーリエ係数は以下の式によって求められます。
\(
v(t) = a_0 + \sum_{k=1}^\infty {a_k \cos kωt + b_k \sin kωt}
\)
\(a_0 = \frac{1}{2π} \int_0^{2π} v(θ)dθ \)
\(a_k = \frac{1}{π} \int_0^{2π} v(θ) \cos kθ dθ\)
\(b_k = \frac{1}{π} \int_0^{2π} v(θ) \sin kθ dθ\)
※上式では積分の下限をθ=0としていますが、積分範囲は一周期であればどこでも問題ありません。
解析例(矩形波解析)
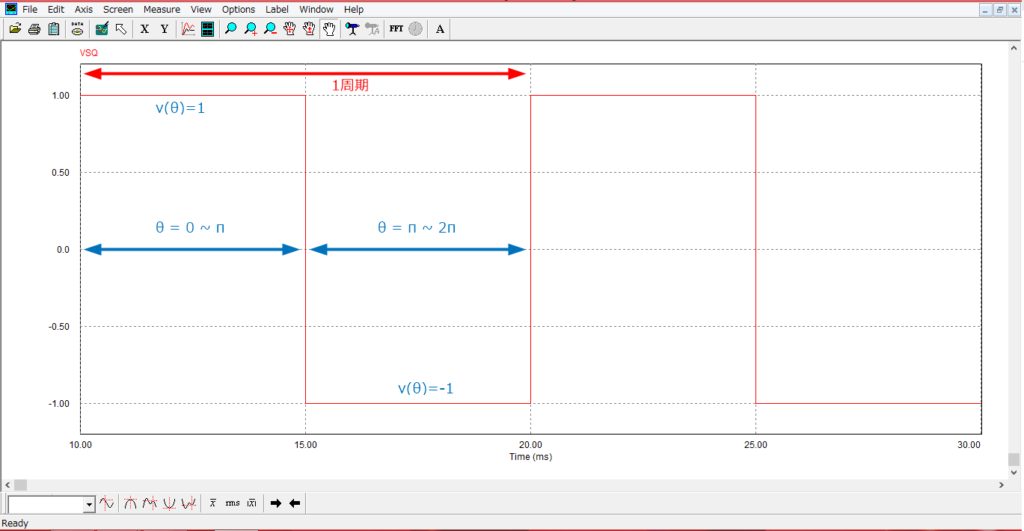
解析の例として、以下の式で表される矩形波 v(θ)のフーリエ級数展開を行ってみましょう。
\(
v(θ)=
\{
\begin{matrix}
1 \quad 0≦θ≦π\\
-1 \quad π<θ≦2π
\end{matrix}
\)
矩形波のフーリエ級数展開
\(a_0 = \frac{1}{2π} \int_0^{2π} v(θ)dθ =\frac{1}{2π} \{\int_0^{π} 1dθ + \int_{π}^{2π} (-1)dθ\} = 0 \)
\(a_k = \frac{1}{π} \int_0^{2π} v(θ) \cos kθ dθ \\
\quad =\frac{1}{π} \{\int_0^{π} \cos kθ dθ + \int_{π}^{2π} (- \cos kθ)dθ\}
= \frac{1}{π} \{ \left [\ \frac{1}{k} \sin kθ \right]^π_0 – \left [\ \frac{1}{k} \sin kθ \right]^2π_π \}
= 0
\)
\(b_k = \frac{1}{π} \int_0^{2π} v(θ) \sin kθ dθ \\
\quad =\frac{1}{π} \{\int_0^{π} \sin kθ dθ + \int_{π}^{2π} (- \sin kθ)dθ\}
= \frac{1}{π} \{ \left [\ – \frac{1}{k} \cos kθ \right]^π_0 + \left [\ \frac{1}{k} \cos kθ \right]^2π_π \}\\
\quad= \frac{1}{π} ( – \frac{1}{k} \cos kπ + \frac{1}{k} + \frac{1}{k} \cos 2kπ – \frac{1}{k} \cos kπ )
= \frac{2}{kπ} (1 – \cos kπ )
\)
(※上記の数式はスクロールできます)
ここで、kが偶数か奇数かによって、上記の計算結果が変わってきますので、両方の場合を見てみます。
【kが奇数】
つまり、\(k = 2m – 1\) では \( \cos kπ = 1\) ⇒ \( 1 – \cos kπ = 0\)
【kが偶数】
つまり\(k = 2m\) では \( \cos kπ = -1\) ⇒ \( 1 – \cos kπ = 2\)
以上をまとめて、\(k = 2m – 1\)を使って表すと以下のようになります。
\( b_{2m-1} = \frac{4}{(2m-1)π} , m = 1,2,3,・・・\)
上記のフーリエ級数を使って、\(a_0,a_k,b_k\)を使って\(v(θ)\)をフーリエ級数展開すると以下の(☆)式のようになります。
\(
v(θ) = \frac{4}{π} \sum_{m=1}^\infty {\frac{1}{2m-1} \sin (2m-1)θ}\\
\quad = \frac{4}{π}(\sinθ + \frac{1}{3} \sin3θ + \frac{1}{5} sin5θ + \frac{1}{7} \sin7θ + ・・・)・・・(☆)
\)
(※上記の数式はスクロールできます)
シミュレーション①~計算結果の確認~
まずは、今回の解析対象の矩形波をFFTして上式の(☆)の結果と一致するかを確認してみましょう。
PSIMのFFT機能についてはこちらの記事をご覧ください。
シミュレーション回路と結果の矩形波は以下のようになります。
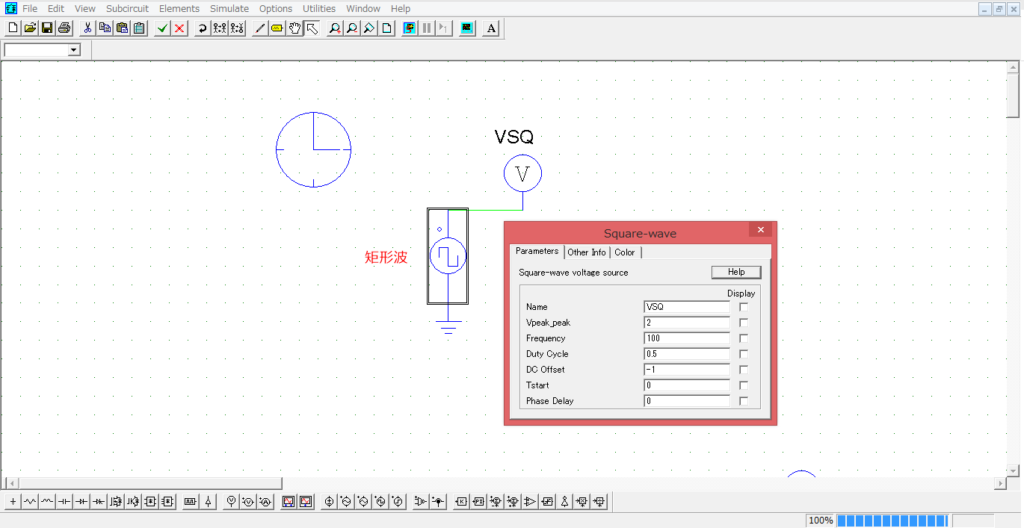
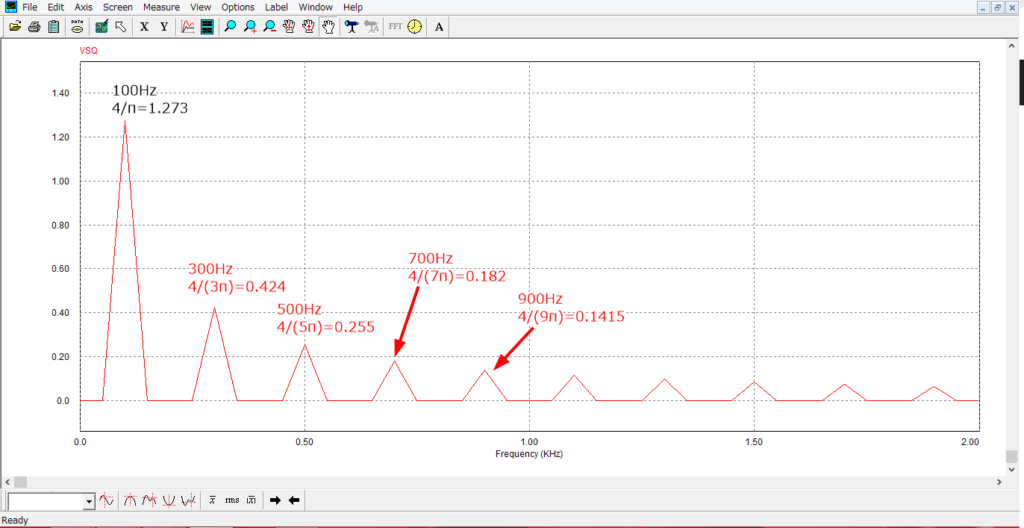
FFT結果は以下になります。
(☆)で計算した結果通りの周波数および振幅がスペクトルとして観測できることが確認できます。
シミュレーション②~正弦波の重ね合わせと元波形との比較~
次に(☆)を使って、元の矩形波を再現できるかどうかを確認してみましょう。
シミュレーションモデルが以下になります。
(☆)式を基に振幅と周波数の異なる正弦波電圧信号源のブロックを使用して生成してそれぞれ加算しています。なお、下図ではsinθ,sin3θ,sin5θの項を加算した場合のシミュレーションモデルを示しています。
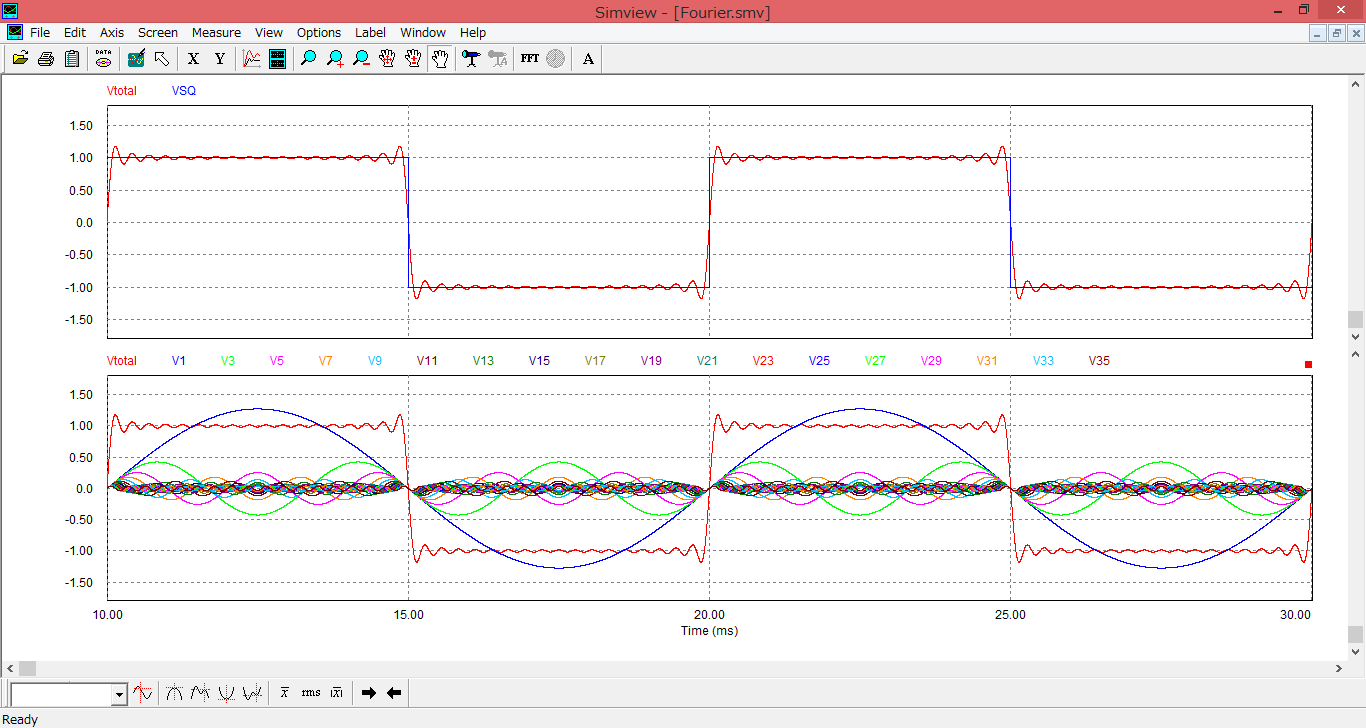
元の矩形波をVSQのスコープで観測、(☆)式をを重ね合わせた波形をVtotalのスコープで観測しています。
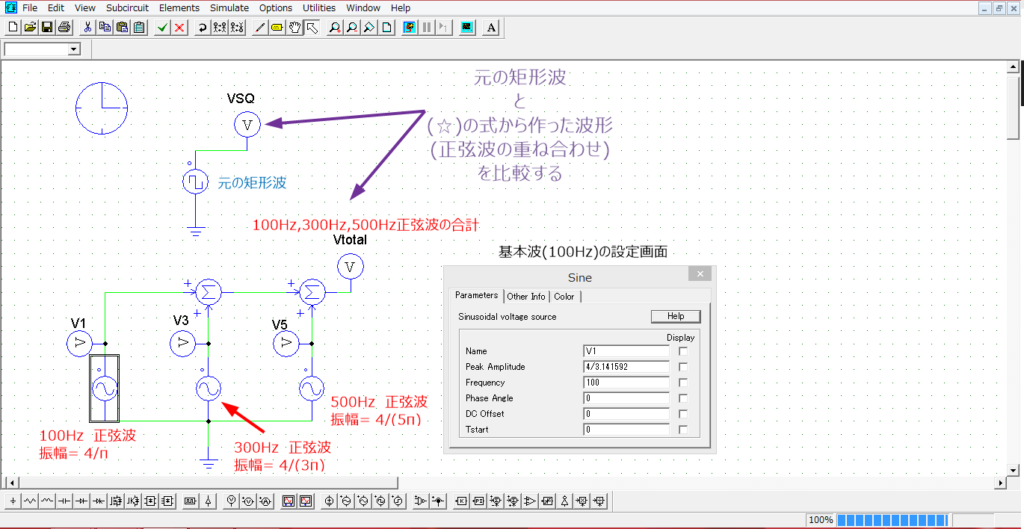
結果が下図のようになります。
1段目の波形が(☆)式の波形と元の矩形波の比較になります。
おおまかに、ではありますが元の矩形波を再現していることが確認できます。
2段目の波形が(☆)式の各項の正弦波と重ね合わせた後の波形(1段目の波形と同様)となっています。
上図のシミュレーションモデルの通り、sinθ,sin3θ,sin5θの項を加算しているため、100Hz、300Hz、500Hzの正弦波が重なり合わさって、赤い波形が生成されていることを示しています。
このように、(☆)式においてm=3、つまり3つの項(100Hz、300Hz、500Hz)のみの加算の場合、傾向としては元の矩形波を再現しているものの、まだまだ誤差がある状態です。
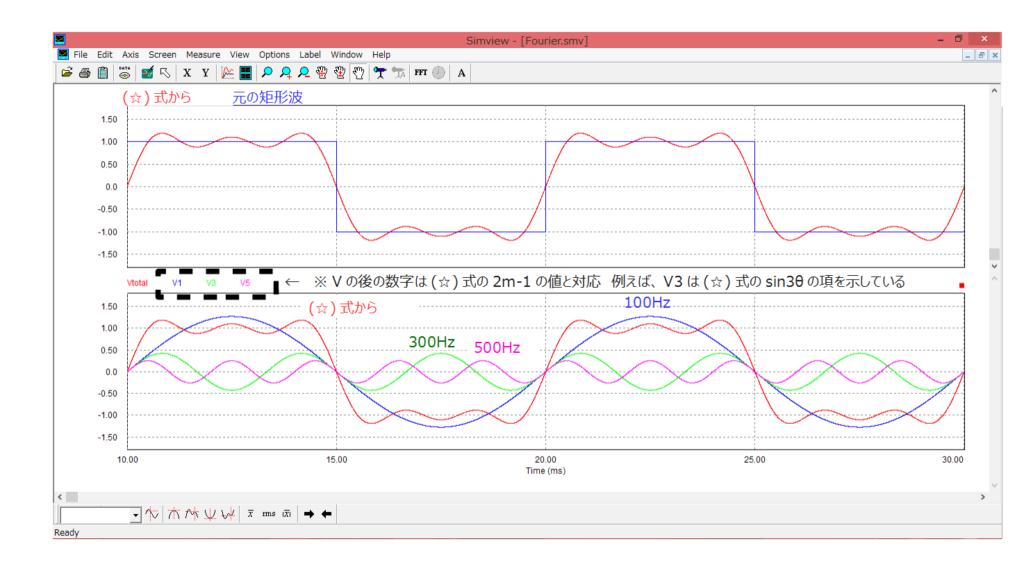
次の波形は(☆)式においてm=8、つまり1500Hzまでを加算した場合の波形になります。
m=3の場合と比較して、だいぶ元の波形に近づいてきました。
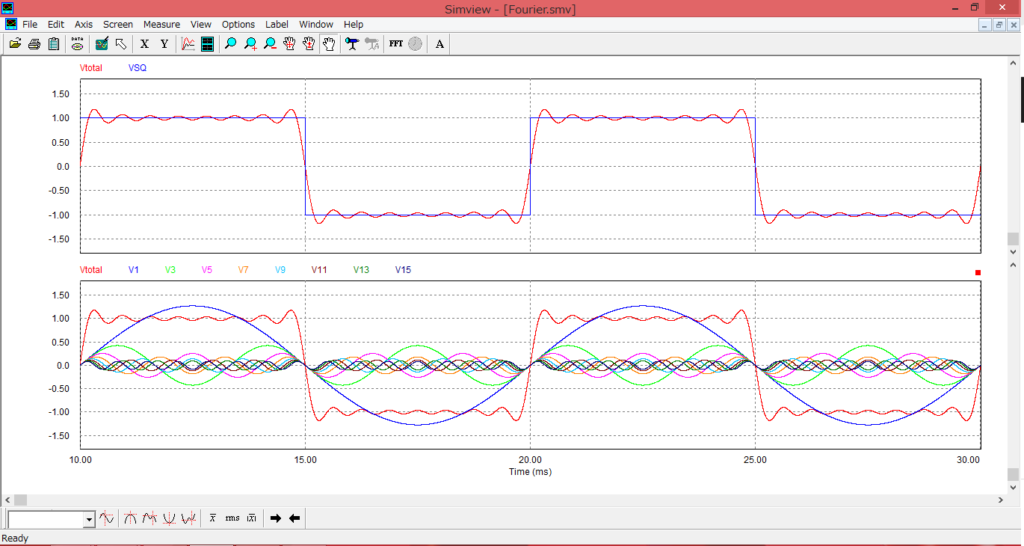
さらにmの値を増加して、m=18の場合の結果が以下になります。
精度よく元の波形を再現できていることが確認できます。
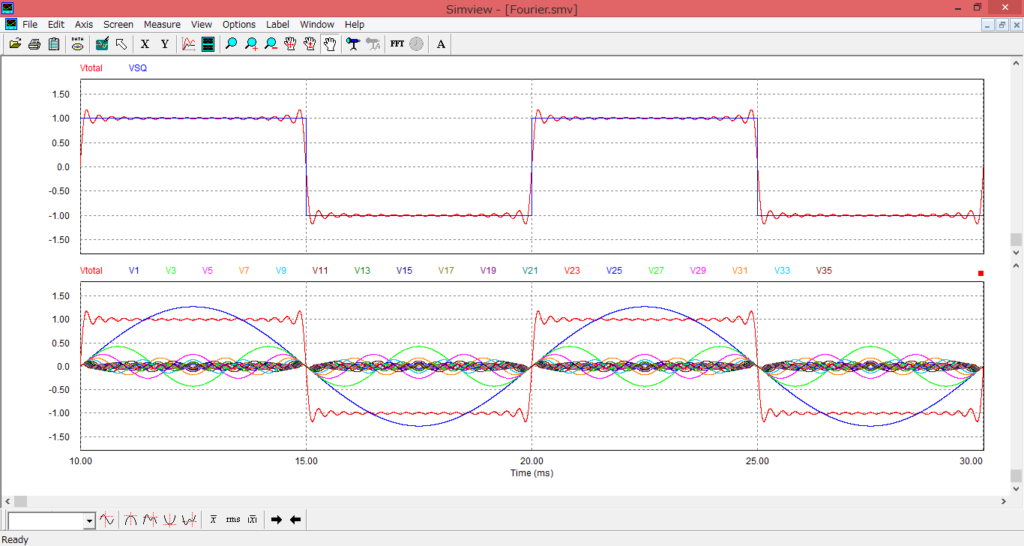
このようにmを増加する、つまり波形を再現する際に使用する周波数成分を増やしていくにつれて、元の波形の再現度が向上することが分かりました。
以上で、フーリエ級数展開の定義、使用方法および実際の非正弦波を対象にした解析の方法、フーリエ級数展開を使用した元波形の再現やその際の注意点についての解説になります。
お疲れさまでした!

コメント