本記事では過渡応答と並び制御系の評価を行う上で重要な指標である、周波数応答の導出方法とRC回路を対象にした具体的な解析方法について解説を行っています。
周波数応答とは
一般的に下図に示すRC回路に正弦波(電圧)入力を加えると十分に時間が経過した状態での出力電圧は振幅/位相ずれは異なるが入力と同じ周波数の正弦波になります。
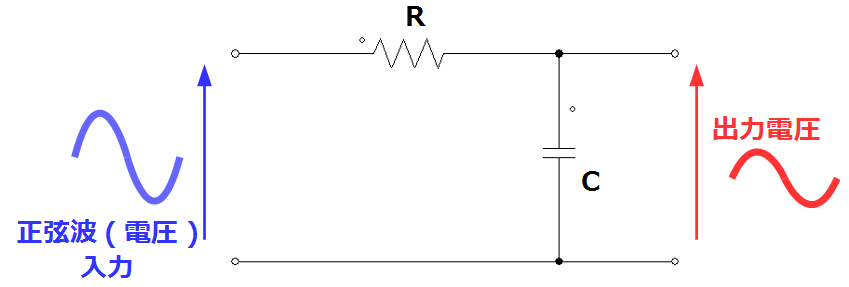
このように伝達関数\(G(s)\)の要素や制御系に正弦波関数\(A \sin ωt \)を入力すると定常状態で出力と入力は同じ正弦波の信号となり、振幅と位相のずれは伝達関数と入力信号の角周波数によって決まります。
これは以下のように説明することができます。
対象の伝達関数\(G(s)\)、入力\(U(s)\)、出力\(X(s)\)が以下のように逆ラプラス変換できるとすると
\[L^{-1}[G(s)]=g(t)、L^{-1}[U(s)]=u(t)、L^{-1}[X(s)]=x(t)\]
※\(L^{-1}[ ]\)は逆ラプラス変換を表します。
\[X(s) = G(s)U(s)・・・(1)\]
の関係があるため、入力\(u(t)\)に対して出力\(x(t)\)は以下の合成積のラプラス変換を用いて、(2)式のようになります。
【合成積のラプラス変換】
2つの関数\(f(t)、g(t)\)について、
\[h(t) = \int_{0}^{t} f(t-τ)g(τ) dτ\]
を\(f(t)、g(t)\)の合成積といい、記号\(f*g\)で表す。
それぞれの関数\(f(t)、g(t)\)のラプラス変換を\(F(s)、G(s)\)とすると
\[L[f*g] = F(s)G(s)\]
※\(L[ ]\)はラプラス変換を表します。
\[x(t) = \int_{t_0}^{t} g(t-τ)u(τ) dτ・・・(2) \]
十分に時間が経過した後のx(t)は(2)式の入力が加わる時刻を移動させることで(3)式のように考えることができます。
\[x(t) = \int_{-\infty}^{t} g(t-τ)u(τ) dτ ・・・(3)\]
ここで、\(t-τ=σ\)と変数変換すると、(4)式のようになります。
\[x(t) = \int_{0}^{\infty} g(σ)u(t-σ) dσ ・・・(4)\]
入力\(u(t)\)を\(A(\cosωt+j\sinωt)\)と考えて、オイラーの公式から\(Ae^{jωt}\)とすると(5)式のようになります。
\[x(t) = \int_{0}^{\infty} g(σ)Ae^{jω(t-σ)} dσ \\ =Ae^{jωt}\int_{0}^{\infty} g(σ)e^{-jωσ} dσ ・・・(5)\]
(5)式で以下の(6)式は伝達関数\(G(s)\)において\(s=jω\)と置いたものとなっている。
\[G(jω)=\int_{0}^{\infty} g(σ)e^{-jωσ} dσ ・・・(6)\]
【参考・ラプラス変換公式】
\[F(s) = \int_0^{\infty} f(t) e^{-st} dt \]
※こちらの記事も参考にしてください
この\(G(jω)\)を\(G(s)\)と区別して周波数伝達関数(または周波数応答関数)といいます。
\(G(jω)\)を用いて出力\(x(t)\)の定常値は以下のように表されます。
\[x(t)=Ae^{jωt}G(jω) ・・・(7)\]
ここで、\(G(jω)\)は複素数であるため絶対値\(M\)と偏角出力\( \phi \)は以下のように表されます。
\[M = |G(jω)|\]
\[\phi = \angle G(jω)\]
これを使って、\(G(jω)\)は以下のようにも表すことができます。
\[G(jω) = Me^{j\phi} ・・・(8)\]
さらに(8)式を使って(7)式を以下のように表すこともできます。
\[x(t) = MAe^{j(ωt+\phi)}= MA\cos(ωt+\phi)+jMA\sin(ωt+\phi)・・・(9)\]
(9)式(=出力)と入力\(u(t)=A(\cosωt+j\sinωt)\)の実部と虚部を比較することで正弦波入力に対する出力応答は振幅\(M\)倍、位相が\( \phi \)ずれ、角周波数は\(ω\)のままであることがわかります。
以上のように正弦波入力に対する出力は入力の角周波数\(ω\)および周波数伝達関数\(G(jω)\)の特性によって決定されます。
ここで、(9)式の振幅比\(M\)をゲイン、位相のずれ\( \phi \)を位相差といいます。
ゲインと位相差は周波数伝達関数\(G(jω)\)固有のもので、要素や制御系の周波数特性を表しています。
このように周波数応答の考え方を用いることで、入力信号に対する、定常状態での出力信号の振幅比や位相のずれによって制御系の特性をとらえることができます。
RC回路を対象にした解析
前章のRC回路を対象にシミュレーションを行った結果を以下に示します。
なお、条件は以下の通りです。
【条件】
□正弦波(電圧)入力:\(100Vpeak、50Hz\)
□抵抗R:\(20Ω\)
□キャパシタ:\(100μF\)
入力に対して、振幅が\(M\)倍、位相遅れ\( \phi \)がある出力が観測されています。
観測された出力電圧の値について考えてみます。
まず、対象のRC回路の伝達関数を求めるため、電圧方程式を以下のように立てます。
\[v_i-v_o=Ri\\i = C \frac{dv_o}{dt}\]
\(i\)を消去してラプラス変換すると以下のようになります。
\[V_i(s)-V_o(s)=RCsV_o(s)\\(1+RCs)V_o = V_i\]
よって伝達関数\(G(s)\)は
\[G(s)=\frac{1}{1+RCs}\]
となります。
今回は周波数伝達関数に着目するため、\(s=jω\)として、展開すると以下のようになります。
\[G(jω)=\frac{1}{1+jωRC}=\\ \frac{1-jωRC}{1+(ωRC)^2}\]
これより、絶対値\(M\)と偏角出力\( \phi \)を計算すると以下のようになります。
\[M = |G(jω)| = \frac{1}{1+(ωRC)^2}\sqrt{1+(ωRC)^2}=\frac{1}{\sqrt{1+(ωRC)^2}}\\
\phi = \angle G(jω) = \tan^{-1}(-ωRC)\]
【条件】に記載の値から\(ω、R、C\)を代入すると以下のようになります。
\[M = \frac{1}{\sqrt{1+(ωRC)^2}}= \frac{1}{\sqrt{1+(2π・50・20・100・10^6)^2}}=0.847\\
\phi = \tan^{-1}(-ωRC) = \tan^{-1}(-2π・50・20・100・10^6) = 31.2 deg \]
これをシミュレーション結果と比較すると。。。
下図の入出力のゼロクロス点の時間差から、位相差は31.2degとなり計算結果と一致します。

ゲイン(振幅比)についても同様に入力に対して、出力が0.847倍になっており、理論値と一致することが確認できました。
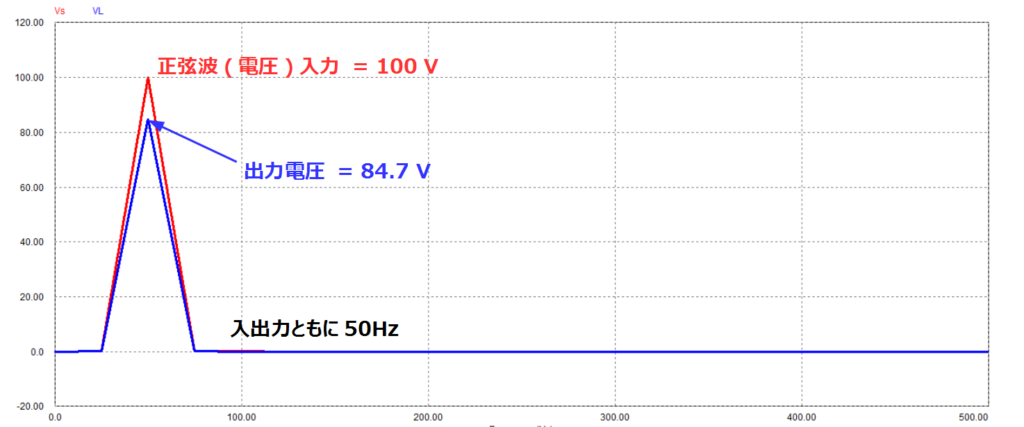
このように対象の伝達関数を利用して周波数応答を求めることができました。
周波数応答を確認することによって、入力信号に対して、出力信号が定常的にどの程度の振幅比、位相ずれをもって観測されるのかを把握することが可能になります。
以上が周波数応答の導出方法とRC回路の解析を対象とした具体例の解説となります。
お疲れさまでした!



コメント