PSIMで学ぶPMSM制御-電圧方程式とフィードフォワード(FF)制御-

本記事ではPMSMに流れる電流を制御する(電流制御)手法として、電圧方程式を基にPMSMに印加するべき電圧を予め計算しておいて、電流を所望の値に制御するFF制御手法を対象に、概要、シミュレーションによる原理検証結果について解説をしています。

PMSMの電圧方程式
電圧方程式の検証(ゼロ電流制御時)
1. シミュレーションモデル
2. シミュレーション結果
電圧方程式の検証(電流を流す場合)
1. シミュレーションモデル
2. シミュレーション結果

PMSMの電圧方程式

PMSMの基本の電圧方程式は以下のように表されます。

\[
\begin{pmatrix}
Vd \\
Vq
\end{pmatrix}＝
\begin{pmatrix}
Ra+pLd&-ωLq \\
ωLd&Ra+pLq
\end{pmatrix}
\begin{pmatrix}
Id \\
Iq
\end{pmatrix}+
\begin{pmatrix}
0\\
ωψ_f
\end{pmatrix}・・・①
\]

\[Vd:d軸電圧、Vq:q軸電圧、Id:d軸電流、Iq:q軸電流、Ra:巻線抵抗、\\
Ld:d軸インダクタンス、Lq:q軸インダクタンス、ψ_f:磁石磁束、\\
ω:電気角周波数、p:微分演算子\]

十分に時間が経過した定常状態では微分項=0として、以下の②式になります。
この②式を用いて以降の解説FF電圧制御について検討していきます。

\[
\begin{pmatrix}
Vd \\
Vq
\end{pmatrix}＝
\begin{pmatrix}
Ra&-ωLq \\
ωLd&Ra
\end{pmatrix}
\begin{pmatrix}
Id \\
Iq
\end{pmatrix}+
\begin{pmatrix}
0\\
ωψ_f
\end{pmatrix}・・・②
\]

電圧方程式の検証(ゼロ電流制御時)

シミュレーションモデル

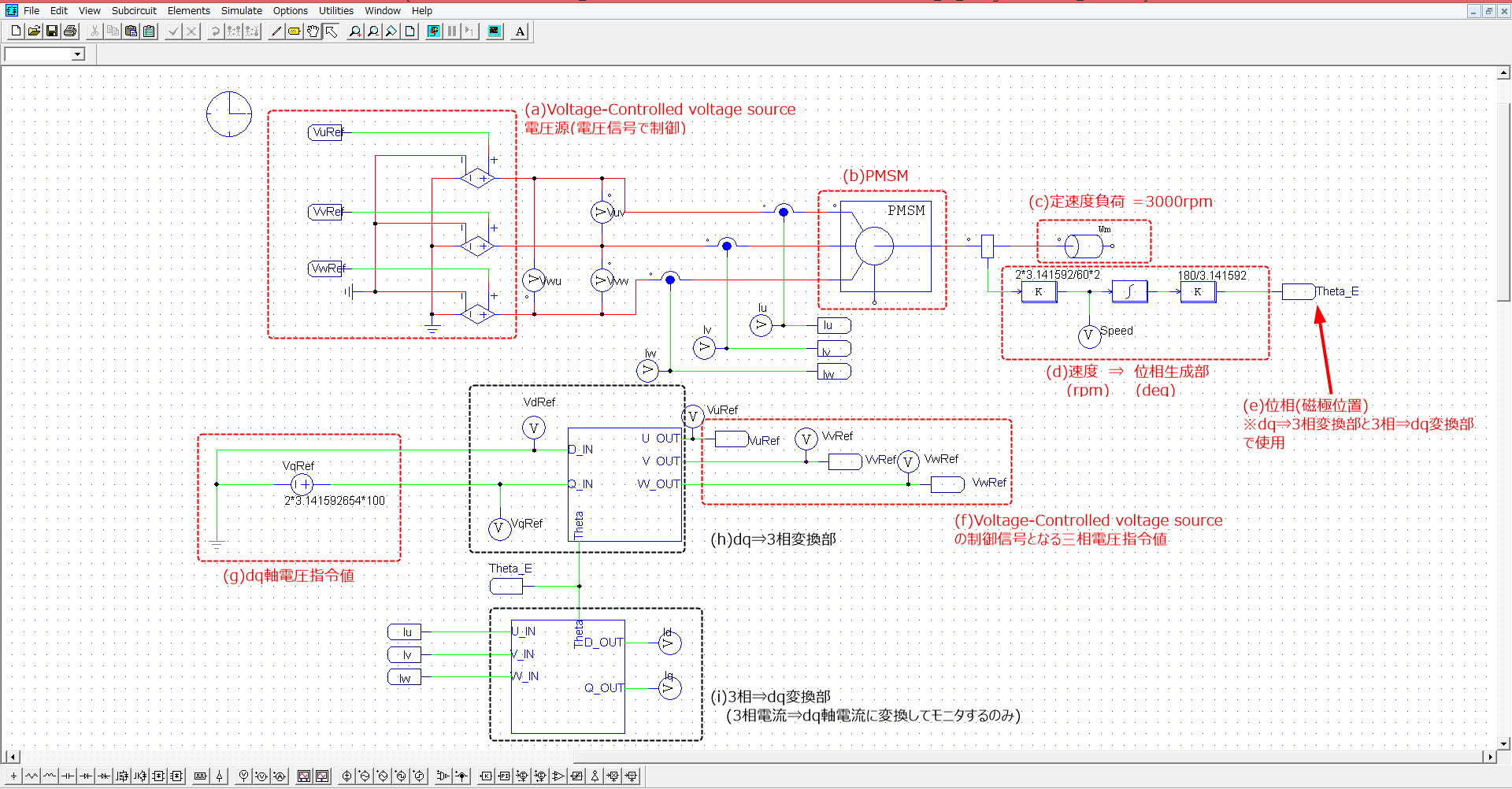
※以下、解説の()内のアルファベットは下図シミュレーションモデルの各ブロックと対応しているため、参考にしてください。

使用するシミュレーションモデルを以下に示します。(b)PMSMを(c)定速度負荷で一定回転数にした状態で、電圧を印加します。電圧の印加には、(a)Voltage-controlled voltage sourceブロックを使用します。このブロックは与えた制御信号(電圧信号)と相似な波形を出力する電圧源になります。この時、(f)制御信号(電圧信号)は(g)dq軸電圧指令値を(h)dq⇒3相変換することにより与えます。

シミュレーションモデルの各ブロックの条件、以下のようになります。
\[【(b)PMSM】\\
　Rs: 0.5(Ω)\\
　Ld: 0.027(H)\\
　Lq: 0.027(H)\\
　Vpk/krpm:296.1921959　(①、②におけるψf=1.0相当)\\
　No. of Poles P: 4\\
　Moment of Inertia: 0.0179 (kg*m2)\\
　Mech. Time Constant: 10\\
　Torque Flag:1：出力あり\\
　Master/Slave: 1：マスタ\\ \]

\[【(c)定速度負荷】\\
　Constant Speed(rpm):3000(電気角周波数ω = 628.319 rad/s)\\
　Moment of Inertia:0\]
\[【(g)dq軸電圧指令値】\]
　(g)dq軸電圧指令値は流したい電流に応じて、②式から決定することとします。まずはdq軸電流をともに0Aとする場合(ゼロ電流制御時)を考えてみましょう。②式から与えるべきdq軸電圧指令値VdRef,VqRefは以下③式になります。

\[
\begin{pmatrix}
U \\
V \\
W
\end{pmatrix}＝
\sqrt{\frac{2}{3}}
\begin{pmatrix}
cosθ&sinθ \\
cos(θ-\frac{2}{3}π)&sin(θ-\frac{2}{3}π) \\
cos(θ+\frac{2}{3}π)&sin(θ+\frac{2}{3}π)
\end{pmatrix}
\begin{pmatrix}
d \\
q
\end{pmatrix}・・・④(h)
\]

\[
\begin{pmatrix}
d \\
q
\end{pmatrix}＝
\sqrt{\frac{2}{3}}
\begin{pmatrix}
cosθ&cos(θ-\frac{2}{3}π)&cos(θ+\frac{2}{3}π)\\
sinθ&sin(θ-\frac{2}{3}π) &sin(θ+\frac{2}{3}π)
\end{pmatrix}
\begin{pmatrix}
U \\
V \\
W
\end{pmatrix}・・・④(i)
\]

シミュレーション結果

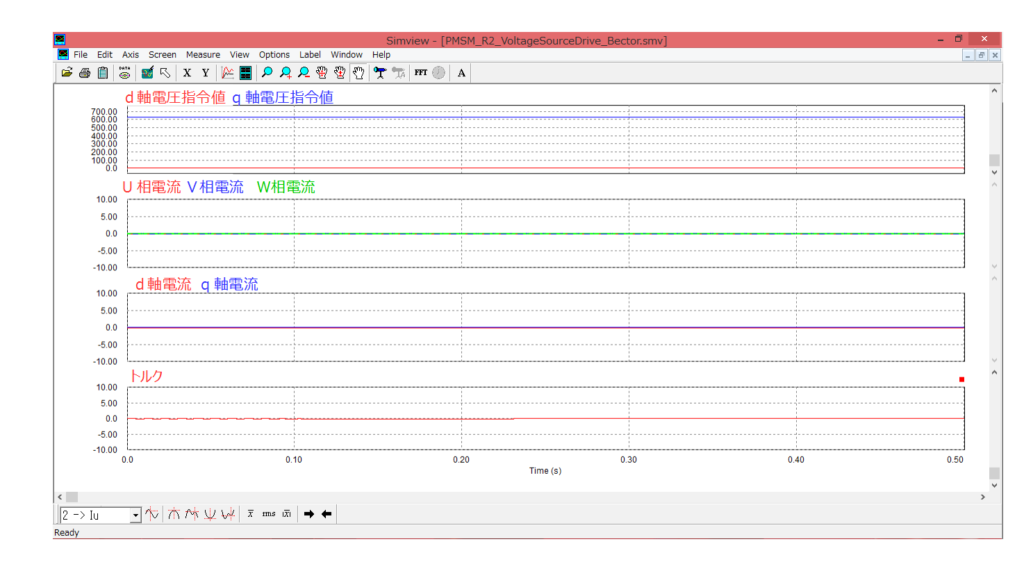
シミュレーションの結果を以下に示します。事前の計算通り、d軸電圧指令値=0V,q軸電圧指令値=628.319Vとすることにより、dq軸電流(U~W相電流)=0Aに制御できていることを確認できます。
また、dq軸電流が0Aであるため、トルクも0Nmであることがわかります。

電圧方程式の検証(電流を流す場合)

シミュレーションモデル

次にdq軸電流0Aからスタートしてd軸電流は0Aに保ったまま、q軸電流のみ0A⇒10Aにスロープ状に(今回は0.25sかけて変化するように)立ち上げるようにdq軸電圧指令値を与えてみましょう。この時のdq軸電流指令値は以下のようになります。
【(g)dq軸電圧指令値】
　スタートのdq軸電流 =0Aの条件は③の通りです。最終値のd軸電流＝0A,q軸電流＝10Aの条件は以下の⑤式になります。そのため、以下のような電圧変化を0.25sかけて行うように電圧指令値を与えることになります。\[\\d軸電圧：0 V　⇒　-169.15 V\\
　q軸電圧：628.318 V　⇒　633.32 V\]

\[
\begin{pmatrix}
VdRef \\
VqRef
\end{pmatrix}＝
\begin{pmatrix}
Ra&-ωLq \\
ωLd&Ra
\end{pmatrix}
\begin{pmatrix}
Id \\
Iq
\end{pmatrix}+
\begin{pmatrix}
0\\
ωψ_f
\end{pmatrix}\\
=
\begin{pmatrix}
0.5&-628.319*0.027 \\
628.319*0.027&0.5
\end{pmatrix}
\begin{pmatrix}
0 \\
10
\end{pmatrix}+
\begin{pmatrix}
0\\
628.319 * 1.0
\end{pmatrix}\\
=
\begin{pmatrix}
-169.15\\
633.32
\end{pmatrix}・・・⑤
\]

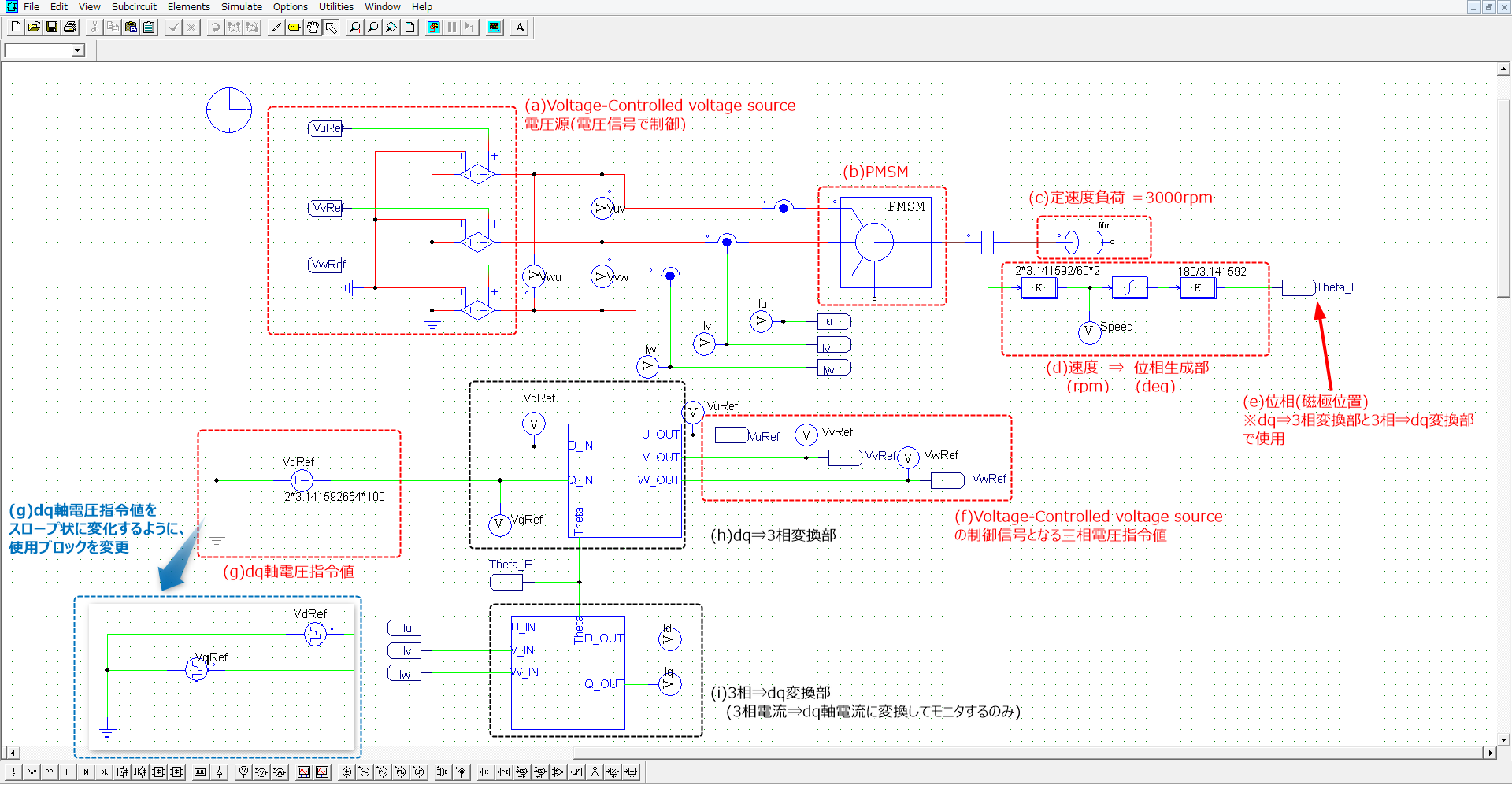
シミュレーションモデルは下図の通りで、基本的にはdq軸電流=0になるようにdq軸電圧指令値を与えていた前章と同じですが、(g)dq軸電圧指令値のみ青枠で囲んだブロックに変更しています。
青枠部のブロックはPiecewise Linear(区分線形電源)ブロックで設定した時刻で線形に変化する電圧信号を生成することができます。設定はdq軸それぞれ以下のように設定しています。

【Piecewise Linear(区分線形電源)】
　シミュレーション開始時(0s)⇒0.1sまではdq軸電流=0Aの条件、0.1s⇒0.35sの区間で0.25sの時間をかけてq軸電流を0⇒10Aに変化させられるように⑤式で設定した電圧になるようにそれぞれ設定0.35s以降はそのままの状態を継続、となるようにPiecewise Linearを以下のように設定します。
※繰り返しは行わないため、Frequency=0としてます。
※Values,Timesは数値間にスペースを入れるようにしましょう。
　<d軸電圧 VdRef>
　　Frequency ＝０
　　No. of Points n = 4
Values V1 ..Vn = 0 0 -169.15 -169.15
Times T1..Tn = 0 0.1 0.35 1

　<q軸電圧 VdRef>
　　Frequency ＝０
　　No. of Points n = 4
Values V1 ..Vn = 628.318 628.318 633.32 633.32
Times T1..Tn = 0 0.1 0.35 1

シミュレーション結果

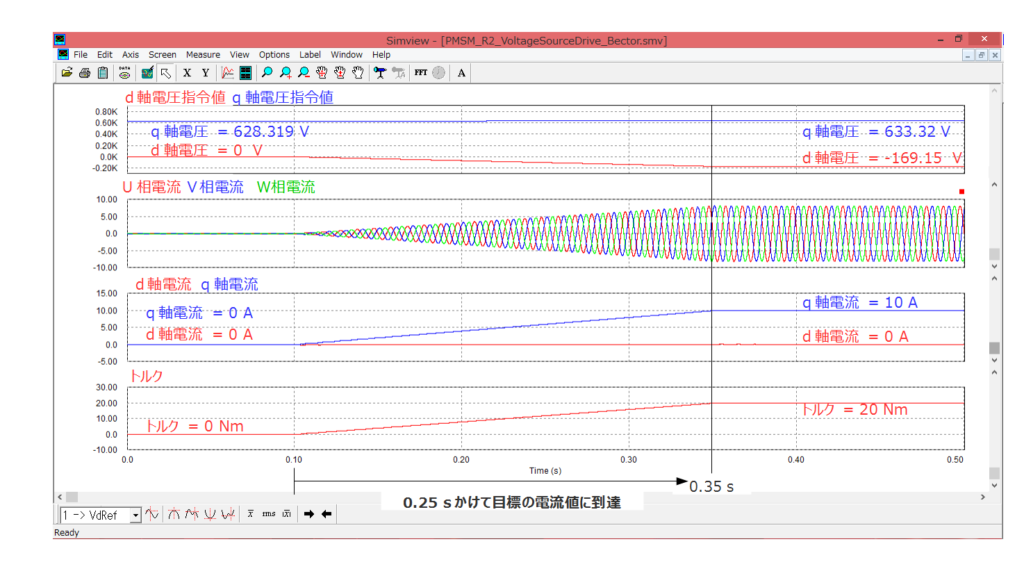
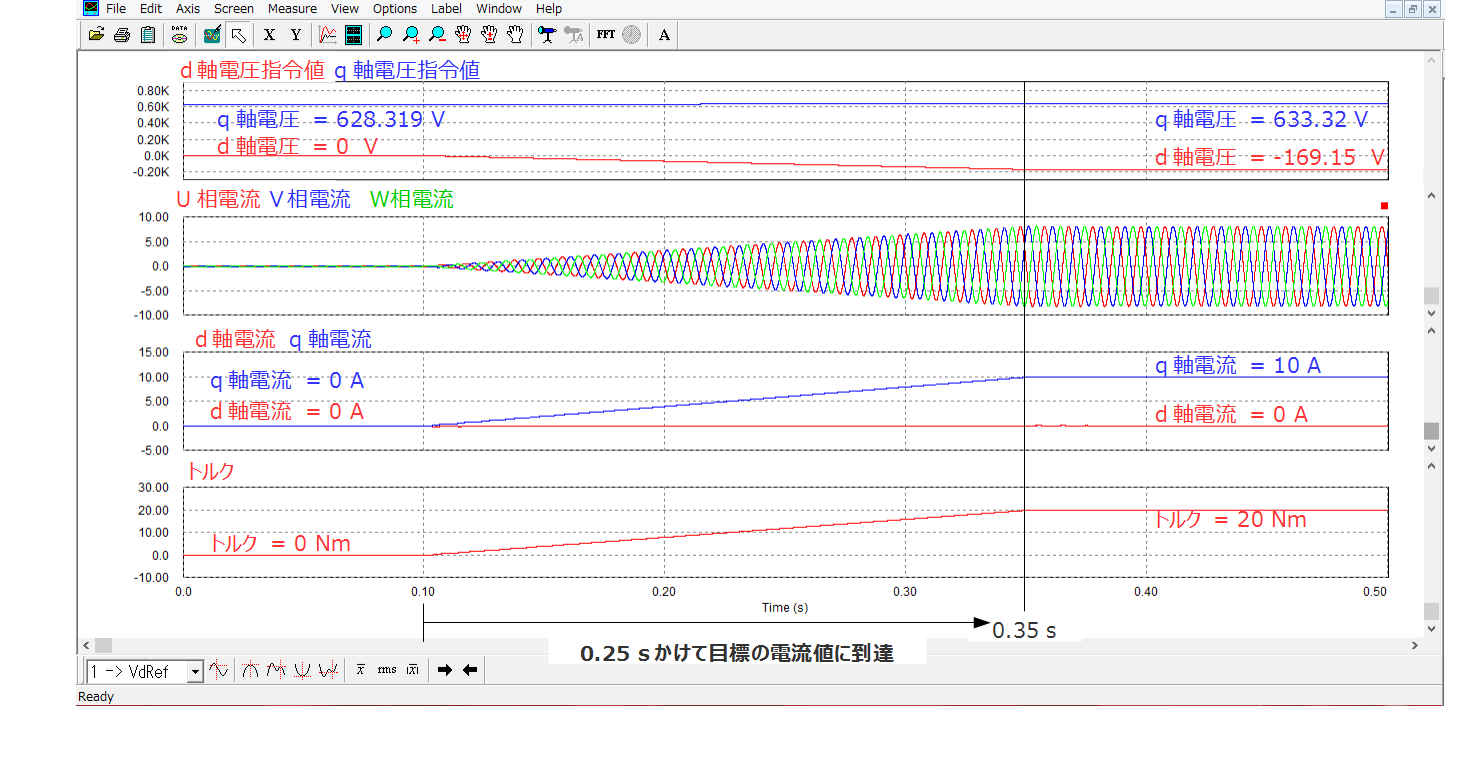
結果が下図のようになります。0s～0.1sの間は③の電圧指令値になっていることによりdq軸電流=0Aになっています。0.1s～0.35sの間でdq軸電圧をそれぞれ⑤で計算した値になるようにスロープ状に増加させていくことで、d軸電流は0Aに保ったまま、q軸電流のみ10Aに増加していることが確認できます。
0.35s以降は電圧指令値を変化させず、そのまま与え続けているため、dq軸電流もそのまま流れ続けています。なお、トルクもq軸電流=10Aであるため、以下の式により20Nmであることが分かります。
(※d軸電流=0A,かつLd=LqのPMSMのため、リラクタンストルク=0)

$$ T = Pn\{ψ_f+(Ld-Lq)Id\}Iq　= 2 * 1.0 * 10 = 20 Nm$$