本記事ではフィードフォワード制御(以降、FF制御)の問題点とそれを受けて、フィードバック制御(以降、FB制御)が必要な理由について説明した後、これらの内容をPMSM制御を例としたシミュレーションを行うことでより詳しく解説しています。
FF制御の問題点
FF制御のおさらい
まずはPMSM制御を例としたシミュレーションを行って、FF制御についておさらいしていきます。
(こちらの記事も参考にしてください)
PMSMに対するFF制御はモータパラメータや動作条件(電気角周波数、dq軸電流)を基に必要な電圧を予め演算しておき、PMSMに印加することで所望の電流値に制御する手法でした。
FF制御は以下のようなブロック図で実現します。
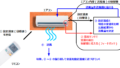
【主回路】
□定速度負荷:PMSMを一定の速度で回転させる
□電圧源:三相電圧指令値(制御回路より)と相似な電圧をPMSMに印加する
□速度センサ:PMSMの回転速度(rpm)を検出する
□電流センサ:PMSMに流れる電流(A)を検出する
□PMSM:定速度負荷で決められた速度で回転、電圧源からの電圧に応じて電流が流れ、トルクを出力
【制御回路】
□速度⇒位相/電気角周波数変換:速度センサで検出した回転速度(rpm)を電気角周波数(rad/s)に変換、また、電気角周波数を積分して位相(deg)を生成
□dq軸電流指令値生成:所望のdq軸電流指令値を生成、FF電圧演算に使用する
□FF電圧演算:以下の①式により、dq軸電流指令値、電気角周波数、モータパラメータから
dq軸電圧指令値を演算する
\[
\begin{pmatrix}
Vd \\
Vq
\end{pmatrix}=
\begin{pmatrix}
Ra&-ωLq \\
ωLd&Ra
\end{pmatrix}
\begin{pmatrix}
Id \\
Iq
\end{pmatrix}+
\begin{pmatrix}
0\\
ωψ_f
\end{pmatrix}・・・①\\
Vd:d軸電圧、Vq:q軸電圧、Id:d軸電流、Iq:q軸電流、Ra:巻線抵抗、\\
Ld:d軸インダクタンス、Lq:q軸インダクタンス、ψ_f:磁石磁束、\\
ω:電気角周波数、p:微分演算子
\]
□dq/三相変換:dq軸電圧指令値を三相電圧指令値に変換
※これが主回路の電圧源(Voltage-Controlled voltage source)に与えられ、PMSMを駆動
つまり、等価的にdq軸電圧指令値をPMSMに与えていることになります。
□三相/dq変換:三相電流をdq軸電流に変換(※ここではモニタ用)

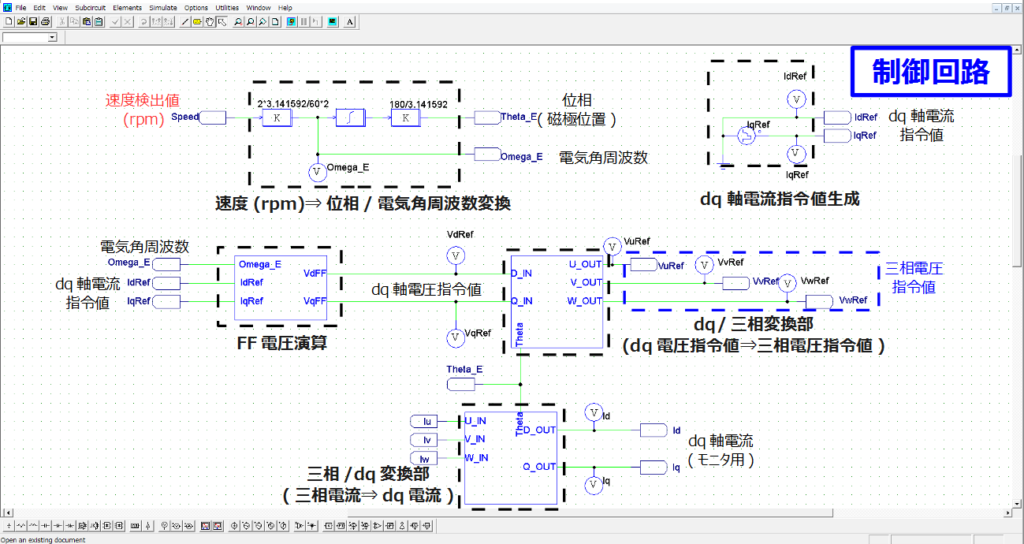
これをPSIM上にシミュレーションモデルとして作成すると主回路は下図のようになります。
PMSMのパラメータや定速度負荷の設定は以下の通りです。
【PMSM】
Rs: 0.5(Ω)
Ld: 0.027(H)
Lq: 0.027(H)
Vpk/krpm:296.1921959 (①におけるψf=1.0相当)
No. of Poles P: 4
Moment of Inertia: 0.0179 (kg*m2)
Mech. Time Constant: 10
Torque Flag:1:出力あり
Master/Slave: 1:マスタ
【定速度負荷】
Constant Speed(rpm):3000(電気角周波数ω = 628.319 rad/s)
Moment of Inertia:0
【電圧源】
電圧指令値と相似な波形を生成できるようにVoltage-Controlled voltage sourceを使用しています。
これにより、等価的にdq⇒三相変換前のdq軸電圧をPMSMに印加できることになります。

制御回路は下図のようになります。まず、速度⇒位相/電気角周波数変換は上記の通りで、dq軸電流指令値は以下のように与えています。
【dq軸電流指令値生成】
d軸電流指令値は0Aに固定
q軸電流指令値は0.1sまで0A、 0.1s~0.35の区間で10Aにスロープ状に増加、 0.35s以降は10A
Subcircuitが三カ所ありますが、それぞれ以下のようになっています。
※Subcircuitの使い方はこちらをご覧ください
【FF電圧演算】
上記の①式の通りdq軸電圧指令値を演算しています。
【dq/三相変換部】
\[
\begin{pmatrix}
U \\
V \\
W
\end{pmatrix}=
\sqrt{\frac{2}{3}}
\begin{pmatrix}
cosθ&sinθ \\
cos(θ-\frac{2}{3}π)&sin(θ-\frac{2}{3}π) \\
cos(θ+\frac{2}{3}π)&sin(θ+\frac{2}{3}π)
\end{pmatrix}
\begin{pmatrix}
d \\
q
\end{pmatrix}・・・②
\]
【三相/dq変換部】
\[
\begin{pmatrix}
d \\
q
\end{pmatrix}=
\sqrt{\frac{2}{3}}
\begin{pmatrix}
cosθ&cos(θ-\frac{2}{3}π)&cos(θ+\frac{2}{3}π)\\
sinθ&sin(θ-\frac{2}{3}π) &sin(θ+\frac{2}{3}π)
\end{pmatrix}
\begin{pmatrix}
U \\
V \\
W
\end{pmatrix}・・・③
\]
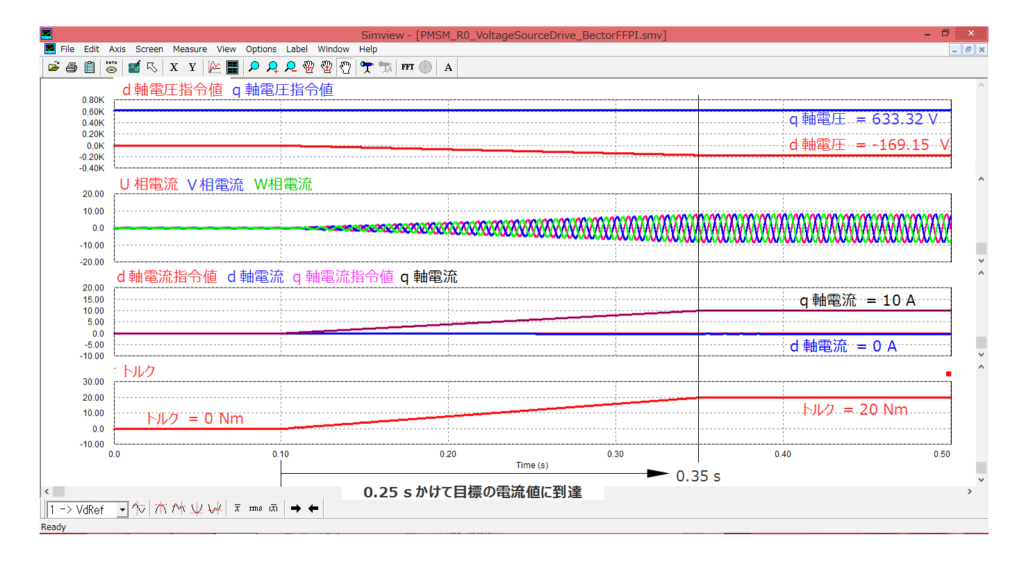
シミュレーション結果は以下のようになります。
電流が指令値の通り、d軸電流は0Aのまま、q軸電流は0.1s~0.35sの区間で10Aに増加して、その後、10Aのまま制御されています。
ここまでが理想的なFF制御で制御器(FF電圧演算に使用するモータパラメータ)と主回路のPMSMでモータのパラメータに差異がない場合であれば、所望の値通りに制御できていることを示しています。
問題点
次にFF制御の問題点について解説していきます。FF制御の問題点としてはこちらの記事にもあるように実際のシステムの内容と制御が把握している内容に誤差があった場合、所望の状態に制御できないことが挙げられます。
一例として前述のシミュレーションについて見てみましょう。
PMSMのモータパラメータに応じてFF電圧演算を行って、PMSMにFF電圧を印加することで所望の動作点に制御していました。しかし、下図に示すようにPMSMと、制御回路のFF電圧演算のパラメータに誤差があった場合はどうなるでしょうか。

これをシミュレーションした結果が以下になります。
基本的な設定は前述の内容と同じですが、一点PMSMモデルのq軸インダクタンスのみ以下のように変更しています。
【PMSM】
Lq: 0.027(H) ⇒ 0.0216(H)
※前述の内容よりも20%減少させた値に設定しています。
※制御回路のFF電圧演算はLq=0.027(H)として計算を行っています。
つまり主回路と制御回路の間でLqの値のみ20%誤差があることになります。
この状態でシミュレーションした結果が以下になります。先程のシミュレーションでは電流が指令値通りに制御できていたのに対して、今回はq軸電流が指令値10Aに対して、12.5Aと指令値よりも大きな値となっています。
この理由について解説していきます。まず、制御回路のFF電圧演算では以下の式④でFF電圧を計算します。
\[
\begin{pmatrix}
VdRef \\
VqRef
\end{pmatrix}=
\begin{pmatrix}
Ra&-ωLqC \\
ωLd&Ra
\end{pmatrix}
\begin{pmatrix}
Id \\
Iq
\end{pmatrix}+
\begin{pmatrix}
0\\
ωψ_f
\end{pmatrix}\\
=
\begin{pmatrix}
0.5&-628.319*0.027 \\
628.319*0.027&0.5
\end{pmatrix}
\begin{pmatrix}
0 \\
10
\end{pmatrix}+
\begin{pmatrix}
0\\
628.319 * 1.0
\end{pmatrix}\\
=
\begin{pmatrix}
-169.15\\
633.32
\end{pmatrix}・・・④\]
※今回のケースでは主回路と制御回路でLqの値が異なるため、Lqに関してのみ、制御回路内で扱う場合はLqC、主回路で扱う場合はLqと書き分けています。
一方、主回路のPMSMにId=0A,Iq=10A流すために必要な電圧は以下⑤のようになります。
\[
\begin{pmatrix}
VdRef \\
VqRef
\end{pmatrix}=
\begin{pmatrix}
Ra&-ωLq \\
ωLd&Ra
\end{pmatrix}
\begin{pmatrix}
Id \\
Iq
\end{pmatrix}+
\begin{pmatrix}
0\\
ωψ_f
\end{pmatrix}\\
=
\begin{pmatrix}
0.5&-628.319*0.0216 \\
628.319*0.027&0.5
\end{pmatrix}
\begin{pmatrix}
0 \\
10
\end{pmatrix}+
\begin{pmatrix}
0\\
628.319 * 1.0
\end{pmatrix}\\
=
\begin{pmatrix}
-135.72\\
633.32
\end{pmatrix}・・・⑤\]
このように主回路のPMSMには-135.72(V) 印加すれば良いのに対して、-169.15 (V)印加してしまっていることにより、指令値よりも大きく電流が流れる結果となります。
(FF制御では現状の動作状態に応じて、出力電圧を変えることができないため、指令値より大きく電流が流れていた場合でも修正ができない)
以上のシミュレーションから主回路と制御回路の間でパラメータの誤差があることにより、FF制御のみでは所望の状態に必ずしも制御できない、というFF制御の問題点が分かりました。

FB制御の導入
前章までに述べたFF制御の問題点を解決するため、FB制御を追加してシミュレーションを行ってみます。こちらの記事にも記載してありますが、FB制御を行うことにより、目標値とシステムの出力結果(今回のケースですと目標値=dq軸電流指令値,システムの出力結果=dq軸電流)をずれなく制御することが可能になります。
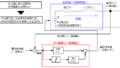
下図に示したようなブロック図を基にシミュレーションモデルを構築していきます。
基本的にはFF制御のみの場合のブロック図と同じですが、以下の三点が異なります
①PI制御を追加 ※これがFB制御を行います。
②モニタのみであったdq軸電流をPI制御に入力、dq軸電流指令値をPI制御にも入力
③PI制御の出力とFF電圧演算の出力を加算して電圧指令値(dq軸電圧指令値)を生成
特にPI制御器はFB制御の根幹を担うブロックで目標値とシステムの出力結果の差(偏差といいます)を逐次計算。比例制御、積分制御を行って偏差を0にするための電圧指令値を生成していきます。
※PI制御の詳細は別記事に記載します。
制御回路の構成も大きくは変わらず、基本的には前章の内容と同じで、FF電圧演算が所望の動作点(dq軸電流)にするための電圧指令値を演算してPMSMに印加します。ただし、今回はPI制御器がdq軸電流を監視して指令値からずれた分、電圧指令値を修正して目標値とシステムの出力結果を一致させます。

シミュレーションモデルは以下のようになります。
主回路部分は前章と同じため省略しています。パラメータも基本的には同じですが、Lqのみ20%減少させた0.0217(H)である点にご注意ください。
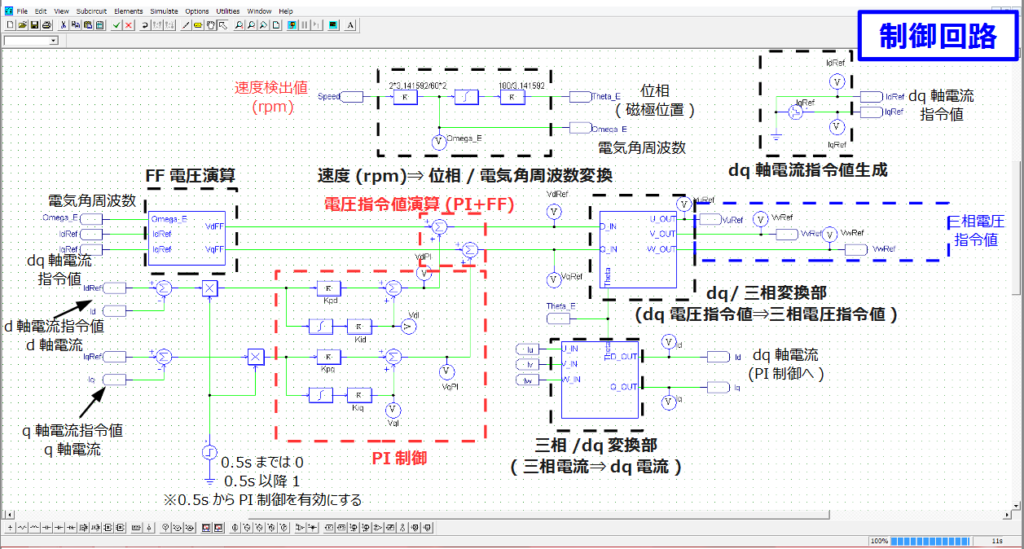
制御回路のシミュレーションモデルが下図になります。
こちらもPI制御と電圧指令値演算(PI+FF)がある点以外は前章と同じです。この二点のみ詳細を以下に示します。
【PI制御】
目標値であるdq軸電流指令値とシステムの出力結果であるdq軸電流を比較して偏差を計算
偏差に比例ゲインKpを掛けてP成分を生成(P制御)
偏差を積分し、積分ゲインKiを掛けてI成分を生成(I制御)
P成分とI成分を加算
ただし、今回のシミュレーションではPI制御あり/なしの影響を比較するため、PI制御は0.5sから開始
0.5secより前は偏差を0にして、PI制御は機能させない
【電圧指令値演算】
PI制御の出力とFF電圧演算の出力を加算して、dq軸電圧指令値を生成
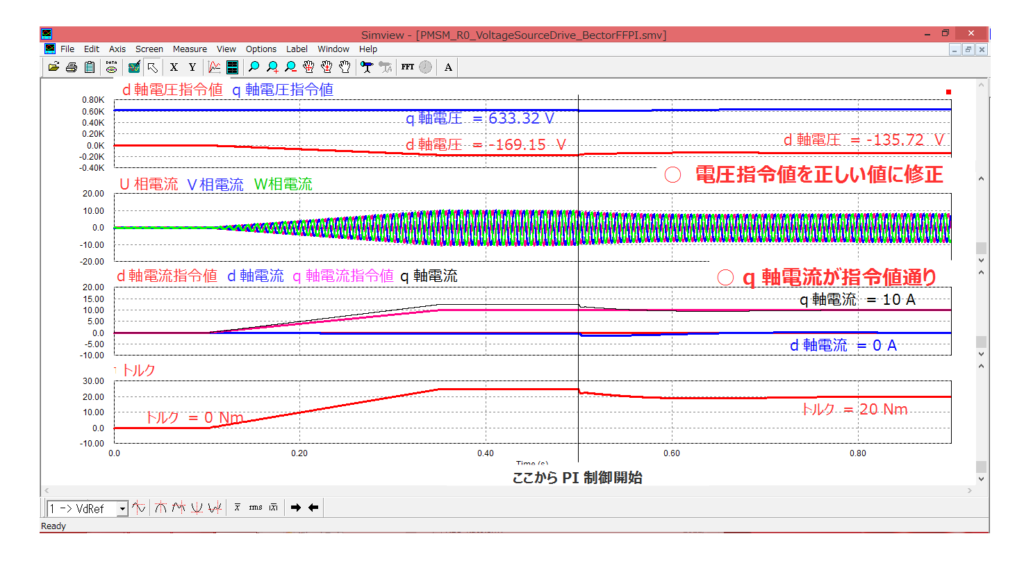
シミュレーション結果が以下になります。
FF制御のみの0.5sまでは前章に示したように電流指令値と電流が一致していません。
0.5sからPI制御を開始すると、FF電圧演算のみで決まっていたdq軸電圧指令値が徐々にFB制御(PI制御)の効果によって修正され、それとともにdq軸電流も次第に指令値に追従するようになってきます。
(0.5sまではFF電圧演算のみのため、④式の電圧を出力、0.5s以降はPI制御により、PMSMに本来印加するべき電圧、つまり⑤式の電圧を出力)
このようにFB制御を行うことにより、FF制御のみでは修正できなかった主回路と制御回路の間のパラメータ誤差で発生する悪影響を無くすことができました。
このようにFF制御とFB制御を組み合わせて制御を行うことにより、
実際のシステムの内容と制御が把握している内容に誤差があった場合、所望の状態に制御できない
といったFF制御のデメリットをFB制御が偏差を0にするように動作することで補いつつ、
システムの内容を基に予め必要な電圧を計算しておくことで目標値付近に速く、容易に動作点を制御できる
といったFF制御のメリットを活かすことができるようになります。
FF制御、FB制御を適切に組み合わせて用いることが制御の基本となってきます。
以上が、実際のPMSM制御を題材としたFF制御の問題点の説明、FB制御の適用方法、FF、FB制御の組み合わせ方の解説になります。
お疲れさまでした!
コメント